题目内容
 如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC分别交DE、BE于点G、H,则∠EFC=
如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC分别交DE、BE于点G、H,则∠EFC=考点:线段垂直平分线的性质,等腰三角形的判定与性质,直角三角形斜边上的中线
专题:
分析:由已知条件,根据等边对等角,线段的垂直平分线的性质以及直角三角形斜边上的中线的性质得到等腰三角形,根据等边对等角,利用三角形的内角和定理得出∠EFC的度数.
解答:解:∵AB=AC,
∴△ABC是等腰三角形.
∵DE垂直平分AB,
∴AE=BE.
∴△ABE是等腰三角形;
∵BE⊥AC,
∴∠△ABE是等腰直角三角形,
∴∠BAC=∠ABE=45°,
∴△ADE和△BDE是等腰直角三角形;
∵AF⊥BC,
∴BF=FC,
∴在RT△BEC中,EF=BF,EF=FC,
∴△BEF和△EFC是等腰三角形.
∴图中共有 6个等腰三角形,
∵△EFC是等腰三角形,
∴∠C=∠FEC,
∴∠EFC+2∠C=180°,
∵∠BAC+2∠C=180°,
∴∠EFC=∠BAC=45°.
故答案为45°,6.
∴△ABC是等腰三角形.
∵DE垂直平分AB,
∴AE=BE.
∴△ABE是等腰三角形;
∵BE⊥AC,
∴∠△ABE是等腰直角三角形,
∴∠BAC=∠ABE=45°,
∴△ADE和△BDE是等腰直角三角形;
∵AF⊥BC,
∴BF=FC,
∴在RT△BEC中,EF=BF,EF=FC,
∴△BEF和△EFC是等腰三角形.
∴图中共有 6个等腰三角形,
∵△EFC是等腰三角形,
∴∠C=∠FEC,
∴∠EFC+2∠C=180°,
∵∠BAC+2∠C=180°,
∴∠EFC=∠BAC=45°.
故答案为45°,6.
点评:本题考查的是线段垂直平分线的性质,等腰三角形的判定与性质,直角三角形斜边上的中线的性质及三角形内角和定理;熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目
若一个三角形的三边为5,12,13,那么这个三角形的外接圆的半径是( )
| A、5 | B、6 | C、6.5 | D、不能确定 |
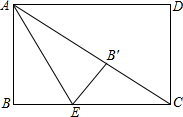 如图,长方形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把△ABE沿着AE折叠,使点B恰好落在AC上的点B′处,则BE的长为
如图,长方形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把△ABE沿着AE折叠,使点B恰好落在AC上的点B′处,则BE的长为 已知四边形ABCD的面积为4,∠ADC=∠B=90°,AD=DC,求点D到AB的距离DF.
已知四边形ABCD的面积为4,∠ADC=∠B=90°,AD=DC,求点D到AB的距离DF. 如图,AE∥BF∥CG∥DH,AB=
如图,AE∥BF∥CG∥DH,AB=