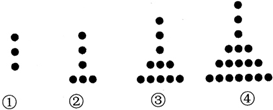
题目内容
14.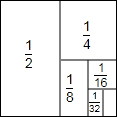 阅读材料:如图,把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的矩形(长方形),按着把面积为$\frac{1}{2}$的矩形等分成两个面积为$\frac{1}{4}$的矩形,再把面积为$\frac{1}{4}$的矩形等分成两个面积为$\frac{1}{8}$ 的矩形,如此进行下去.我们可以利用图形展示的规律将累加式进行化简:$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+A+\frac{1}{{2}^{n}}$.
阅读材料:如图,把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的矩形(长方形),按着把面积为$\frac{1}{2}$的矩形等分成两个面积为$\frac{1}{4}$的矩形,再把面积为$\frac{1}{4}$的矩形等分成两个面积为$\frac{1}{8}$ 的矩形,如此进行下去.我们可以利用图形展示的规律将累加式进行化简:$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+A+\frac{1}{{2}^{n}}$.例如:由于$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{32}=1$,所以$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}=1-\frac{1}{32}$.
完成解答:
①类比上面推理将累加式$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+A+\frac{1}{{2}^{n}}$化简为1-$\frac{1}{{2}^{n}}$;
②利用上面的解题方法化简累加式1+2+22+23+24+A+2n=2n+1-1;
③化简累加式:$\frac{5}{2}+\frac{17}{4}+\frac{65}{8}+\frac{257}{16}+…+\frac{(2n)^{2}+1}{{{2}^{n}}_{\;}}$=2n+1-1-$\frac{1}{{2}^{n}}$.
分析 ①由$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}=1-\frac{1}{32}$类比得出答案即可;
②设S=1+2+22+23+24+A+2n,则2S=2+22+23+24+A+2n+1,把两个式子作差,进一步求得S的数值得出答案即可;
③由①②计算的规律,把原式拆分,进一步计算得出答案即可.
解答 解:①$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+A+\frac{1}{{2}^{n}}$
=1-$\frac{1}{{2}^{n}}$.
②S=1+2+22+23+24+A+2n,
2S=2+22+23+24+A+2n+1,
2S-S=2n+1-1,S=2n+1-1,
即1+2+22+23+24+A+2n=2n+1-1.
③原式=2+4+8+…+2n+$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+A+\frac{1}{{2}^{n}}$化
=2n+1-2+1-$\frac{1}{{2}^{n}}$.
=2n+1-1-$\frac{1}{{2}^{n}}$.
故答案为:1-$\frac{1}{{2}^{n}}$;2n+1-1;2n+1-1-$\frac{1}{{2}^{n}}$.
点评 此题考查图形的变化规律,找出数字之间的运算规律,利用数字之间的运算规律解决问题.

练习册系列答案
相关题目
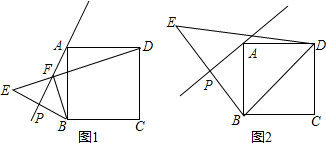
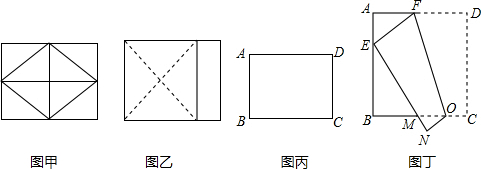
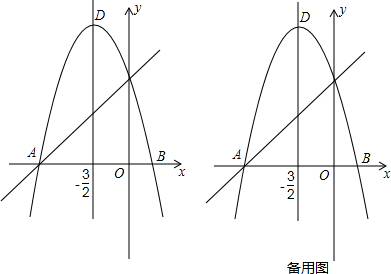
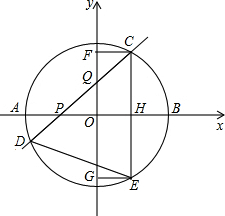 如图,⊙O的圆心O在坐标原点,直径AB=8,点P是直径AB上的一个动点(点P不与A、B两点重合),过点P的直线PQ的解析式为y=x+m,当直线PQ交y轴于Q,交⊙O于C、D两点时,过点C作CE垂直于x轴交⊙O于点E,过点E作EG垂直于y轴,垂足为G,过点C作CF垂直于y轴,垂足为F,连接DE.
如图,⊙O的圆心O在坐标原点,直径AB=8,点P是直径AB上的一个动点(点P不与A、B两点重合),过点P的直线PQ的解析式为y=x+m,当直线PQ交y轴于Q,交⊙O于C、D两点时,过点C作CE垂直于x轴交⊙O于点E,过点E作EG垂直于y轴,垂足为G,过点C作CF垂直于y轴,垂足为F,连接DE.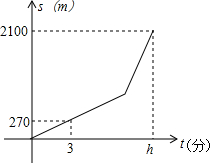 小明从家到学校,开始步行,后来跑步,小明离家的路程S(m)与所用时间t(分)之间的关系如图所示.
小明从家到学校,开始步行,后来跑步,小明离家的路程S(m)与所用时间t(分)之间的关系如图所示.