题目内容
2.课堂上老师提出这样一个问题:你能用手中的矩形纸片尽可能大的折出一个菱形吗?有两位同学很快折出了各自不同的菱形,如甲、乙两图: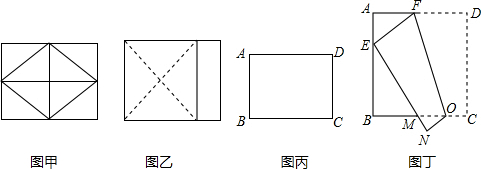
(1)如果该矩形纸片的长为8,宽为6,则甲、乙两图中的菱形周长分别为:20,24.(直接写出答案)
(2)这时老师说,这两位同学折出的菱形周长都不是最大的,聪明的你能够想出最大的菱形应该怎样折出来吗?如丙图所示:在矩形ABCD中,设AB=6,AD=8,请你在图中画出周长最大的菱形的示意图,标注上适当的字母,并求出这个菱形的周长.
(3)借题发挥:如图丁,在正方形ABCD中,AB=6,若折叠该正方形,使得点D落在AB边上的点E处,折痕FG交AD于点F,交BC于点G,边DC折叠后EH与BC交于点M,设AE=a,试探究△EBM的周长与a的取值无关.
分析 (1)由菱形的周长公式边长×4求得;
(2)以BD为对角线,E、F分别在AD,BC上,且EF垂直平分BD,在Rt△ABE中,由勾股定理可求得BE的长,即为DE的长,则周长=4DE;
(3)由于AE=a,BE=6-a,则在Rt△AEF中,根据勾股定理可求得AF的值,由角的关系可求得△AEF∽△BME⇒$\frac{AF}{BE}$=$\frac{AE}{BM}$=$\frac{EF}{EM}$,求得BM,EM的长,则周长=12,所以与a的取值无关.
解答 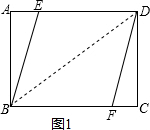 解:(1)甲菱形的边长=$\sqrt{{4}^{2}{+3}^{2}}$=5,
解:(1)甲菱形的边长=$\sqrt{{4}^{2}{+3}^{2}}$=5,
∴甲菱形的周长=5×4=20,
∵乙菱形是正方形,边长为6,则其周长=6×4=24,
故答案为:20,24;
(2)如图1设线段ED的长为x.
∵四边形BFDE是菱形∴ED=BE=x
又∵矩形ABCD中AB=6,AD=8,
∴AE=8-x,
在Rt△ABE中AE2+AB2=BE2,
∴(8-x)2+62=x2,
解之得:x=$\frac{25}{4}$∴ED=$\frac{25}{4}$
∴菱形EBFD的周长=$\frac{25}{4}$×4=25,
(3)如图2:,由折叠的性质得:DF=EF,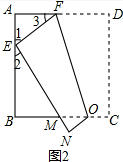
设线段DF的长为x,则EF=x
∵AD=6,
∴AF=6-x,
∵AB=6,
∴AE=a,∴BE=6-a,
在Rt△AEF中有AE2+AF2=EF2
∴a2+(6-x)2=x2,
解得:x=$\frac{{a}^{2}+36}{12}$,
∴AF=6-x=$\frac{36{-a}^{2}}{12}$
在矩形ABCD中由于对折,
∴∠D=∠FEM=90°,∴∠1+∠2=90°
又∵∠A=∠B=90°
∴∠1+∠3=90°
∴∠2=∠3
∴△AEF∽△BME,
∴$\frac{AF}{BE}$=$\frac{AE}{BM}$=$\frac{EF}{EM}$,
∴BM=$\frac{12a}{6+a}$,EM=$\frac{{a}^{2}+36}{6+a}$,
∴△BME的周长=BM+EM+BE=12,
∴△BME的周长为12,与a的取值无关.
点评 本题考查了翻折的性质:对应角相等,对应边相等,以及菱形和正方形、矩形的性质,勾股定理,相似三角形的判定和性质,三角形的周长的求法等知识点.

 阅读快车系列答案
阅读快车系列答案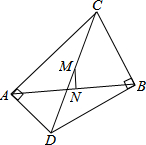 如图,∠CAD和∠CBD都是直角,M是CD的中点,N是AB的中点.求证:直线MN是AB的垂直平分线.
如图,∠CAD和∠CBD都是直角,M是CD的中点,N是AB的中点.求证:直线MN是AB的垂直平分线. 已知∠B=90°,AE,CH分别平分∠DAC,∠ACB.求∠H的度数.
已知∠B=90°,AE,CH分别平分∠DAC,∠ACB.求∠H的度数. 如图,5个正方形重叠,重叠部分的顶点正好是下面一个正方形的中心.若每个正方形的边长都是a,则整个图形的周长是12a.
如图,5个正方形重叠,重叠部分的顶点正好是下面一个正方形的中心.若每个正方形的边长都是a,则整个图形的周长是12a.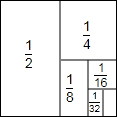 阅读材料:如图,把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的矩形(长方形),按着把面积为$\frac{1}{2}$的矩形等分成两个面积为$\frac{1}{4}$的矩形,再把面积为$\frac{1}{4}$的矩形等分成两个面积为$\frac{1}{8}$ 的矩形,如此进行下去.我们可以利用图形展示的规律将累加式进行化简:$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+A+\frac{1}{{2}^{n}}$.
阅读材料:如图,把一个面积为1的正方形等分成两个面积为$\frac{1}{2}$的矩形(长方形),按着把面积为$\frac{1}{2}$的矩形等分成两个面积为$\frac{1}{4}$的矩形,再把面积为$\frac{1}{4}$的矩形等分成两个面积为$\frac{1}{8}$ 的矩形,如此进行下去.我们可以利用图形展示的规律将累加式进行化简:$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+A+\frac{1}{{2}^{n}}$. 【课本知识】用配方法解方程、切线的性质定理、扇形面积公式.
【课本知识】用配方法解方程、切线的性质定理、扇形面积公式. 如图,在四边形ABCD中,M,N,E,F分别为AD,BC,BD,AC的中点,求证:MN与EF互相平分.
如图,在四边形ABCD中,M,N,E,F分别为AD,BC,BD,AC的中点,求证:MN与EF互相平分.