题目内容
13.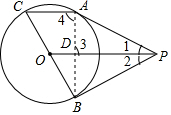 如图,已知:P为⊙O外一点,PA、PB为⊙O的切线,A、B是切点,BC是直径,求证:AC∥OP.
如图,已知:P为⊙O外一点,PA、PB为⊙O的切线,A、B是切点,BC是直径,求证:AC∥OP.证明:连结AB,交OP于点D
∵PA与PB切⊙O于A、B
∴PA=PB,∠1=∠2
∴PD⊥AB,∴∠3=90°
∵BC是⊙O的直径,
∴∠4=90°,∴∠3=∠4,∴AC∥OP
(1)横线上补上应填的条件.
(2)上述证明过程中用到的定理名称或定理的具体内容是(只要求写两个)
①圆周角定理(直径所对的圆周角是直角);②切线长定理(从圆外一点引圆的两条切线,它们的切线长相等,并且这点和圆心的连线平分这两切线的夹角).
分析 (1)根据切线长定理得出PA=PB,∠1=∠2,求出PD⊥AB,求出∠3=90°,根据圆周角定理得出∠4=90°,根据平行线的判定得出即可;
(2)根据证明过程得出即可.
解答 (1)证明:连结AB,交OP于点D
∵PA与PB切⊙O于A、B
∴PA=PB,∠1=∠2
∴PD⊥AB,∴∠3=90°
∵BC是⊙O的直径,
∴∠4=90°,
∴∠3=∠4,
∴AC∥OP,
故答案为:BC是⊙O的直径;
(2)解:故答案为:圆周角定理(直径所对的圆周角是直角),切线长定理(从圆外一点引圆的两条切线,它们的切线长相等,并且这点和圆心的连线平分这两切线的夹角).
点评 本题考查了圆周角定理,切线长定理和平行线的判定等知识点,能熟记定理的内容是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 抛物线y=-x2+(m-1)x+m与y轴交于点(0,3),
抛物线y=-x2+(m-1)x+m与y轴交于点(0,3),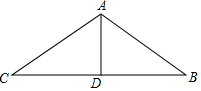 如图,在△ABC中,AB=AC,D是BC边上的中点,∠BAC=110°,求∠C和∠BAD的度数.
如图,在△ABC中,AB=AC,D是BC边上的中点,∠BAC=110°,求∠C和∠BAD的度数.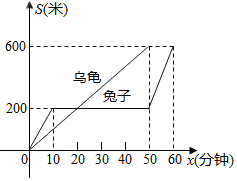 “龟兔赛跑”是同学们熟悉的寓言故事,图中表示路程S(米)与时间t(分)之间的关系,那么可以知道:
“龟兔赛跑”是同学们熟悉的寓言故事,图中表示路程S(米)与时间t(分)之间的关系,那么可以知道: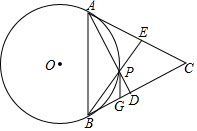 如图,点P是等边三角形ABC内部一个动点,∠APB=120°,⊙O是△APB的外接圆.AP,BP的延长线分别交BC,AC于D,E.
如图,点P是等边三角形ABC内部一个动点,∠APB=120°,⊙O是△APB的外接圆.AP,BP的延长线分别交BC,AC于D,E.