题目内容
解分式方程:
(1)
=
(2)1-
=
.
(1)
| 5 |
| x |
| 3 |
| x-2 |
(2)1-
| 1 |
| x-4 |
| 5-x |
| x-4 |
考点:解分式方程
专题:
分析:(1)先去分母,然后通过去括号、移项、合并同类项解方程即可;
(2)先去分母,然后通过移项、合并同类项解方程即可.
注意:分式方程需要验根.
(2)先去分母,然后通过移项、合并同类项解方程即可.
注意:分式方程需要验根.
解答:解:(1)
=
去分母,得
5x-10=3x,
移项、合并同类项,得
2x=10,
化系数为1,得
x=5,
检验:把x=5代入x(x-2)=5×3≠0∴x=5是原方程的解.
∴x=5是原方程的解.
(2)1-
=
最简公分母是(x-4),则
1×(x-4)-
•(x-4)=
•(x-4),
x-4-1=5-x
2x=10
x=5
检验:把x=5代入x-4=5-4≠0,
∴x=5是原方程的解.
| 5 |
| x |
| 3 |
| x-2 |
去分母,得
5x-10=3x,
移项、合并同类项,得
2x=10,
化系数为1,得
x=5,
检验:把x=5代入x(x-2)=5×3≠0∴x=5是原方程的解.
∴x=5是原方程的解.
(2)1-
| 1 |
| x-4 |
| 5-x |
| x-4 |
最简公分母是(x-4),则
1×(x-4)-
| 1 |
| x-4 |
| 5-x |
| x-4 |
x-4-1=5-x
2x=10
x=5
检验:把x=5代入x-4=5-4≠0,
∴x=5是原方程的解.
点评:本题考查了解分式方程.解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
下列说法错误的是( )
| A、零是绝对值最小的有理数 |
| B、如果两个数互为相反数,那么它们的绝对值相等 |
| C、任何有理数的绝对值都是非负数 |
| D、两个互为相反数的商是-1 |
 如图,⊙O的直径AB与弦CD相交,∠ACD=60°,则∠BAD=
如图,⊙O的直径AB与弦CD相交,∠ACD=60°,则∠BAD=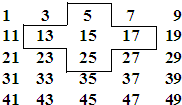 将连续的奇数1、3、5、7、9、…排成如图所示的数阵.
将连续的奇数1、3、5、7、9、…排成如图所示的数阵.