题目内容
1. 如图,直线a∥b,AF:FB=3:5,BC:CD=3:1,则AE:EC为( )
如图,直线a∥b,AF:FB=3:5,BC:CD=3:1,则AE:EC为( )| A. | 5:12 | B. | 9:5 | C. | 12:5 | D. | 3:2 |
分析 利用平行于三角形的一边,并且和其他两边(或两边的延长线)相交的直线,所截得的三角形的三边与原三角形的三边对应成比例可得到$\frac{AF}{BF}$=$\frac{AG}{BD}$=$\frac{3}{5}$,则可设AG=3x,BD=5x,再利用BC:CD=3:1得到CD=$\frac{1}{4}$BD=$\frac{5}{4}$x,然后•根据平行线分线段成比例得到$\frac{AE}{EC}$=$\frac{AG}{CD}$=$\frac{12}{5}$.
解答 解:∵a∥b,
∴$\frac{AF}{BF}$=$\frac{AG}{BD}$=$\frac{3}{5}$,
设AG=3x,BD=5x,
∵BC:CD=3:1,
∴CD=$\frac{1}{4}$BD=$\frac{5}{4}$x,
∵AG∥CD,
∴$\frac{AE}{EC}$=$\frac{AG}{CD}$=$\frac{3x}{\frac{5x}{4}}$=$\frac{12}{5}$.
故选C.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.平行于三角形的一边,并且和其他两边(或两边的延长线)相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
10.方程3x2-5x+1=0的解,正确的是( )
| A. | $x=\frac{{-5±\sqrt{13}}}{6}$ | B. | $x=\frac{{5±\sqrt{13}}}{6}$ | C. | $x=\frac{{-5±\sqrt{13}}}{3}$ | D. | $x=\frac{{5±\sqrt{13}}}{3}$ |
11.数据0,1,1,x,3,4的平均数是2,则这组数据的中位数是( )
| A. | 1 | B. | 2 | C. | 2.5 | D. | 3 |
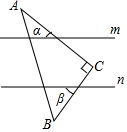 如图,m∥n,直角三角板ABC的直角顶点C在两直线之间,两直角边与两直线相交所形成的锐角分别为α、β,则α+β=90°.
如图,m∥n,直角三角板ABC的直角顶点C在两直线之间,两直角边与两直线相交所形成的锐角分别为α、β,则α+β=90°.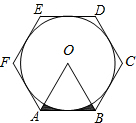 如图,已知半径为2的⊙O内切于正六边形ABCDEF,求图中阴影部分的面积.
如图,已知半径为2的⊙O内切于正六边形ABCDEF,求图中阴影部分的面积. 在压力不变的情况下,某物体承受的压强p(Pa)与它的受力面积S(m2)的反比例函数,其图象如图所示.
在压力不变的情况下,某物体承受的压强p(Pa)与它的受力面积S(m2)的反比例函数,其图象如图所示.