Question

1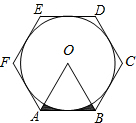．如图，已知半径为2的⊙O内切于正六边形ABCDEF，求图中阴影部分的面积．

Answer 1

分析 作OH⊥AB于H，根据正六边形的性质求出AB、OH，求出△AOB的面积，根据扇形的面积公式求出扇形AOB的面积，计算即可．

解答 解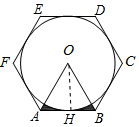：作OH⊥AB于H，
∵六边形ABCDEF是正六边形，
∴∠AOB=60°，
∴AB=OA=2，OH=$\frac{\sqrt{3}}{2}$×2=$\sqrt{3}$，
∴△AOB的面积为：$\frac{1}{2}$×AB×OH=$\sqrt{3}$，
扇形AOB的面积为：$\frac{60π×{2}^{2}}{360}$=$\frac{2}{3}$π，
则图中阴影部分的面积为$\sqrt{3}$-$\frac{2}{3}$π．

点评 本题考查的是正多边形和圆、扇形的面积计算，掌握正六边形的性质、扇形的面积公式是解题的关键．