题目内容
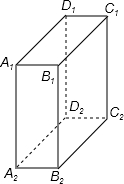 如图,长方体的高为5cm,底面长为4cm,宽为1cm.
如图,长方体的高为5cm,底面长为4cm,宽为1cm.(1)点A1到点C2之间的距离是多少?
(2)若一只蚂蚁从点A2爬到C1,则爬行的最短路程是多少?
考点:平面展开-最短路径问题
专题:
分析:(1)利用勾股定理得出A2C2的长,再利用勾股定理得出A1C2的长;
(2)分类讨论画出解答几何体的部分侧面展开图,利用直角三角形的边的关系容易解得A2C1的值,从而得出其中的最小值.
(2)分类讨论画出解答几何体的部分侧面展开图,利用直角三角形的边的关系容易解得A2C1的值,从而得出其中的最小值.
解答: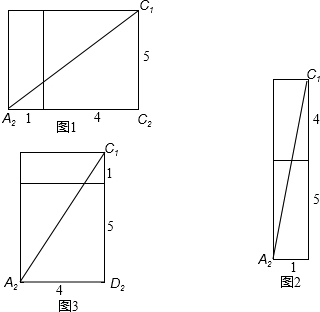 解:(1)∵长方体的高为5cm,底面长为4cm,宽为1cm,
解:(1)∵长方体的高为5cm,底面长为4cm,宽为1cm,
∴A2C2=
=
(cm),
∴A1C2=
=
(cm);
(2)如图1所示:A2C1=
=5
(cm),
如图2所示:A2C1=
=
(cm),
如图3所示:A2C1=
=2
(cm),
∵5
<2
<
,
∴一只蚂蚁从点A2爬到C1,则爬行的最短路程是5
cm.
 解:(1)∵长方体的高为5cm,底面长为4cm,宽为1cm,
解:(1)∵长方体的高为5cm,底面长为4cm,宽为1cm,∴A2C2=
| 42+12 |
| 17 |
∴A1C2=
52+(
|
| 42 |
(2)如图1所示:A2C1=
| 52+52 |
| 2 |
如图2所示:A2C1=
| 92+12 |
| 82 |
如图3所示:A2C1=
| 62+42 |
| 13 |
∵5
| 2 |
| 13 |
| 82 |
∴一只蚂蚁从点A2爬到C1,则爬行的最短路程是5
| 2 |
点评:此题主要考查了勾股定理的应用以及平面展开图最短路径问题,利用分类讨论得出是解题关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
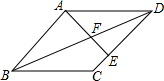 如图,菱形ABCD中,点E在CD上,且DE=2CE,AE交BD于点F,若△DEF的面积为1,则△ADF的面积等于( )
如图,菱形ABCD中,点E在CD上,且DE=2CE,AE交BD于点F,若△DEF的面积为1,则△ADF的面积等于( )A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
 已知直线MN和点P,求作:直线PQ⊥MN,(要求用尺规作图,保留作图痕迹,不要求写作法)
已知直线MN和点P,求作:直线PQ⊥MN,(要求用尺规作图,保留作图痕迹,不要求写作法)
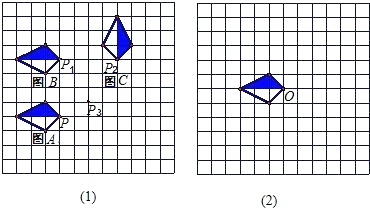
 如图,在△ABC中,AB=AC,四边形ADEF是菱形,求证:BE=CE.
如图,在△ABC中,AB=AC,四边形ADEF是菱形,求证:BE=CE.