题目内容
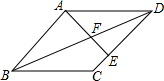 如图,菱形ABCD中,点E在CD上,且DE=2CE,AE交BD于点F,若△DEF的面积为1,则△ADF的面积等于( )
如图,菱形ABCD中,点E在CD上,且DE=2CE,AE交BD于点F,若△DEF的面积为1,则△ADF的面积等于( )A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
考点:菱形的性质
专题:
分析:根据菱形的对角线平分一组对角线可得BD平分∠ADC,再根据角平分线上的点到角的两边距离相等可得点F到AD、CD的距离相等,然后用CE表示出AD,再利用三角形的面积公式列式计算即可得解.
解答:解:在菱形ABCD中,BD平分∠ADC,
∴F到AD、CD的距离相等,
∴DE=2CE,
∴CD=3CE,
∴AD=CD=3CE,
∵△DEF的面积为1,
∴△ADF的面积=1÷2×3=
.
故选C.
∴F到AD、CD的距离相等,
∴DE=2CE,
∴CD=3CE,
∴AD=CD=3CE,
∵△DEF的面积为1,
∴△ADF的面积=1÷2×3=
| 3 |
| 2 |
故选C.
点评:本题考查了菱形的性质,角平分线上的点到角的两边距离相等的性质,等高的三角形的面积的比等于底边的比,熟记性质并用CE表示出AD是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在等式y=kx+4中,当x=2,y=-6,则k的值为( )
| A、-5 | B、-1 | C、1 | D、5 |
若
+|
+2|=0,则yx的值等于( )
| x-2 |
| 3 | y |
| A、-36 | B、-64 |
| C、36 | D、64 |
若点A(a,2)在第二象限,则( )
| A、a≤0 | B、a≥0 |
| C、a<0 | D、a>0 |
已知1≤a≤
,化简
+|a-2|的结果是( )
| 2 |
| a2-2a+1 |
| A、2a-3 | B、2a+3 |
| C、3 | D、1 |
下列各等式中成立的是( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
 如图,△ABC沿射线AC方向平移2cm得到△A′B′C′,若AC=3cm,则A′C=
如图,△ABC沿射线AC方向平移2cm得到△A′B′C′,若AC=3cm,则A′C=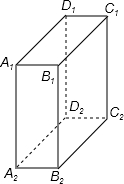 如图,长方体的高为5cm,底面长为4cm,宽为1cm.
如图,长方体的高为5cm,底面长为4cm,宽为1cm.