题目内容
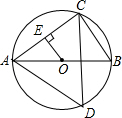 如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,BC=3.
如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,BC=3.(1)求∠ADC的度数;
(2)如果OE⊥AC,垂足为E,求OE的长.
考点:圆周角定理,含30度角的直角三角形,三角形中位线定理,垂径定理
专题:计算题
分析:(1)由AB是⊙O的直径,根据圆周角定理的推论得到∠ACB=90°,在Rt△ABC中,理由∠B的余弦可求出∠B=60°,然后根据圆周角定理得到∠ADC=60°;
(2)由于OE⊥AC,根据垂径定理得到AE=CE,则OE为△ABC的中位线,所以OE=
BC=
.
(2)由于OE⊥AC,根据垂径定理得到AE=CE,则OE为△ABC的中位线,所以OE=
| 1 |
| 2 |
| 3 |
| 2 |
解答:解:(1)∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=6,BC=3,
∴cosB=
=
,
∴∠B=60°,
∴∠ADC=60°;
(2)∵OE⊥AC,
∴AE=CE,
∴OE为△ABC的中位线,
∴OE=
BC=
.
∴∠ACB=90°,
∵AB=6,BC=3,
∴cosB=
| BC |
| AB |
| 1 |
| 2 |
∴∠B=60°,
∴∠ADC=60°;
(2)∵OE⊥AC,
∴AE=CE,
∴OE为△ABC的中位线,
∴OE=
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了垂径定理和锐角三角函数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列运算正确的是( )
| A、x2-x-2=x0 |
| B、x2+x-2=x0 |
| C、x2×x-2=x0 |
| D、x2÷x-2=x0 |
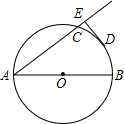 如图,AB、AC分别是⊙O的直径和弦,D为
如图,AB、AC分别是⊙O的直径和弦,D为
 如图,AB为⊙O的直径,点C为⊙O上的一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.试判断CD与⊙O的位置关系,并说明理由.
如图,AB为⊙O的直径,点C为⊙O上的一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.试判断CD与⊙O的位置关系,并说明理由. 如图,直线y=k1x+b与反比例函数
如图,直线y=k1x+b与反比例函数 作图:(保留作图痕迹,不要求写作法)
作图:(保留作图痕迹,不要求写作法)
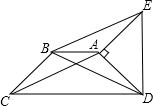 如图,在等腰梯形ABCD中,已知AB∥CD,AD=BC,∠ADC=45°,将腰AD绕A点逆时针旋转90°,得到AE,连接BE、DE、AC、BD.求证:四边形ACBE是平行四边形.
如图,在等腰梯形ABCD中,已知AB∥CD,AD=BC,∠ADC=45°,将腰AD绕A点逆时针旋转90°,得到AE,连接BE、DE、AC、BD.求证:四边形ACBE是平行四边形.