题目内容
若|a|=b+1，b=2，且ab＜0，求4a-|b-2（b+a）+2a|的值．
考点：整式的加减—化简求值,绝对值
专题：计算题
分析：利用绝对值的代数意义及a与b异号，求出a的值，原式绝对值里边去括号合并后，将a与b的值代入计算即可求出值．
解答：解∵|a|=b+1，b=2，
∴|a|=3，即a=±3；
∵ab＜0，∴a=-3，
则4a-|b-2（b+a）+2a|=4a-|b-2b-2a+2a|=4a-|b|=4×（-3）-|2|=-14．
∴|a|=3，即a=±3；
∵ab＜0，∴a=-3，
则4a-|b-2（b+a）+2a|=4a-|b-2b-2a+2a|=4a-|b|=4×（-3）-|2|=-14．
点评：此题考查了整式的加减-化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
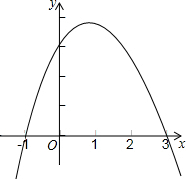二次函数y=ax2+bx+c（a、b、c是常数a≠0）的大致图象如图所示，抛物线交x轴于点（-1，0），（3，0）．若函数y的值随着x的增大而增大，则x的取值范围是（ ）| A、x≤1 | B、x≤-1 |
| C、x≥1 | D、x≥3 |
下列说法中正确的是（ ）
| A、1是单项式 |
| B、单项式m的系数为0，次数为0 |
| C、单项式2a2b的系数是2，次数是2 |
| D、xy-x+y-4的项是xy，x，y，4 |
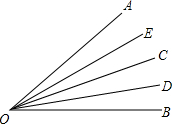已知：如图，∠AOB=40°，OC平分∠AOB，OD、OE分别平分∠BOC和∠AOC．
如图用一张边长为16cm的正方形纸片，在其四个角上减掉四个边长相同的小正方形可做成无盖的长方体盒子．若设减掉的小正方形的边长为xcm，做成的无盖长方体盒子的容积为Vcm2．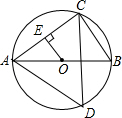
如图，已知AB是⊙O的直径，点C，D在⊙O上，且AB=6，BC=3．