题目内容
点B、C、E在同一直线上,点A、D在直线CE的同侧,AB=AC,EC=ED,∠BAC=∠CED,直线AE、BD交于点F.
(1)如图①,若∠BAC=60°,则∠AFB= ,如图②,若∠BAC=90°,则∠AFB= ;
(2)如图③,若∠BAC=α,则∠AFB= (用含α的 代数式表示)证明这个结论.

(1)如图①,若∠BAC=60°,则∠AFB=
(2)如图③,若∠BAC=α,则∠AFB=

考点:相似三角形的判定与性质
专题:
分析:(1)由题意易得△ABC∽△EDC,进一步证得△BCD∽△ACE,进而可得∠AFB=∠CBD+∠AEC=∠CAE+∠AEC=∠ACB=60°,同理可得,∠AFB的大小;
(2)同(1)的证明可得.
(2)同(1)的证明可得.
解答:解:(1)解:∵AB=AC,EC=ED,∠BAC=∠CED=60°,
∴△ABC∽△EDC,
∴∠CBD=∠CAE,
∴∠AFB=180°-∠CAE-∠BAC-∠ABD
=180°-∠BAC-∠ABC
=∠ACB,
∴∠AFB=60°,
同理可得:∠AFB=45°,
故答案为:60°,45°;
(2)∠AFB=90°-
a,
证明:∵AB=AC,EC=ED,∠BAC=∠CED
∴△ABC∽△EDC,
∴
=
,
∵∠BCD=∠ACE,
∴△BCD∽△ACE,
∴∠CBD=∠CAE.
∠AFB=∠CBD+∠AEC=∠CAE+∠AEC=∠ACB.
∵AB=AC,∠BAC=a,
∴∠ACB=90°-
a,
∴∠AFB=90°-
a.
∴△ABC∽△EDC,
∴∠CBD=∠CAE,
∴∠AFB=180°-∠CAE-∠BAC-∠ABD
=180°-∠BAC-∠ABC
=∠ACB,
∴∠AFB=60°,
同理可得:∠AFB=45°,
故答案为:60°,45°;
(2)∠AFB=90°-
| 1 |
| 2 |
证明:∵AB=AC,EC=ED,∠BAC=∠CED
∴△ABC∽△EDC,
∴
| BC |
| DC |
| AC |
| EC |
∵∠BCD=∠ACE,
∴△BCD∽△ACE,
∴∠CBD=∠CAE.
∠AFB=∠CBD+∠AEC=∠CAE+∠AEC=∠ACB.
∵AB=AC,∠BAC=a,
∴∠ACB=90°-
| 1 |
| 2 |
∴∠AFB=90°-
| 1 |
| 2 |
点评:本题考查了相似三角形的判定和性质以及三角形的外角关系,本题还突出考查从特殊与一般的数学思想和实验研究的能力,让学生经历了动手操作、观察猜想、合情推理、归纳证明等全过程.

练习册系列答案
相关题目
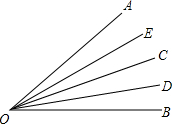 已知:如图,∠AOB=40°,OC平分∠AOB,OD、OE分别平分∠BOC和∠AOC.
已知:如图,∠AOB=40°,OC平分∠AOB,OD、OE分别平分∠BOC和∠AOC.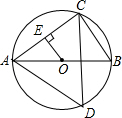 如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,BC=3.
如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,BC=3. 已知:如图,在△ABC中,AB=AC,∠ABC和∠ACB的平分线交于点P.
已知:如图,在△ABC中,AB=AC,∠ABC和∠ACB的平分线交于点P.