题目内容
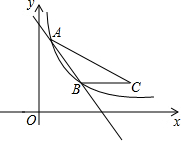 如图,直线y=k1x+b与反比例函数y=
如图,直线y=k1x+b与反比例函数y=| k2 |
| x |
(1)求k1、k2的值;
(2)直接写出k1x+b-
| k2 |
| x |
(3)作BC平行x轴,且BC=AB,连接AC,得到△ABC,再将△ABC沿直线AC翻折,得到△AB′C,若反比例函数y=
| m |
| x |
考点:反比例函数综合题
专题:
分析:(1)首先把A的坐标代入反比例函数的解析式,即可求得k2的值,即求得反比例函数的解析式,然后求得B的坐标,进而利用待定系数法即可求得一次函数的解析式;
(2)k1x+b-
>0即一次函数的值大于反比例函数的值,就是一次函数的图象在反比例函数的图象的上边,求得对应的x的范围即可;
(3)首先求得C的坐标,进而求得AC的中点坐标,根据B与B'关于AC对称求得B'的坐标,则m的范围即可求解.
(2)k1x+b-
| k2 |
| x |
(3)首先求得C的坐标,进而求得AC的中点坐标,根据B与B'关于AC对称求得B'的坐标,则m的范围即可求解.
解答:解:(1)由题意知 k2=1×6=6,
∴反比例函数的解析式为y=
.
又B(a,3)在y=
的图象上,
∴a=2.∴B(2,3).
∵直线y=k1x+b过A(1,6),B(2,3)两点,
∴
∴
∴k1、k2分别为-3和6.
(2)根据图象得:x的取值范围为1<x<2.
(3)AB=
=
,
在BC=AB=
,
C的坐标是:(2+
,3),
则AC的中点的坐标是(
,
),
设B′的坐标是(x,y),
则
=
,且
=
,
解得:x=1+
,y=6,
则B′的坐标是:(2+
,3).
当y=
经过点A时,m=6;
当经过点(1+
,6)时,m=6+6
则m的范围是:6≤m≤6+6
.
∴反比例函数的解析式为y=
| 6 |
| x |
又B(a,3)在y=
| 6 |
| x |
∴a=2.∴B(2,3).
∵直线y=k1x+b过A(1,6),B(2,3)两点,
∴
|
∴
|
∴k1、k2分别为-3和6.
(2)根据图象得:x的取值范围为1<x<2.
(3)AB=
| (2-1)2+(3-6)2 |
| 10 |
在BC=AB=
| 10 |
C的坐标是:(2+
| 10 |
则AC的中点的坐标是(
3+
| ||
| 2 |
| 9 |
| 2 |
设B′的坐标是(x,y),
则
| 2+x |
| 2 |
3+
| ||
| 2 |
| 3+y |
| 2 |
| 9 |
| 2 |
解得:x=1+
| 10 |
则B′的坐标是:(2+
| 10 |
当y=
| m |
| x |
当经过点(1+
| 10 |
| 10 |
则m的范围是:6≤m≤6+6
| 10 |
点评:本题考查了利用待定系数法求反比例函数和一次函数的解析式,利用数形结合解决此类问题,是非常有效的方法,求得B′的坐标是关键.

练习册系列答案
相关题目
如果(a+1)2=9,则a等于( )
| A、2 | B、-4 | C、±3 | D、2或-4 |
 如图用一张边长为16cm的正方形纸片,在其四个角上减掉四个边长相同的小正方形可做成无盖的长方体盒子.若设减掉的小正方形的边长为xcm,做成的无盖长方体盒子的容积为Vcm2.
如图用一张边长为16cm的正方形纸片,在其四个角上减掉四个边长相同的小正方形可做成无盖的长方体盒子.若设减掉的小正方形的边长为xcm,做成的无盖长方体盒子的容积为Vcm2.
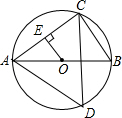 如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,BC=3.
如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,BC=3.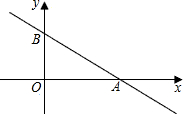 如图:直线y=kx+3与x轴、y轴分别交于A、B两点,
如图:直线y=kx+3与x轴、y轴分别交于A、B两点, 在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题: