题目内容
 如图,AB为⊙O的直径,点C为⊙O上的一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.试判断CD与⊙O的位置关系,并说明理由.
如图,AB为⊙O的直径,点C为⊙O上的一点,若∠BAC=∠CAM,过点C作直线l垂直于射线AM,垂足为点D.试判断CD与⊙O的位置关系,并说明理由.考点:切线的判定
专题:
分析:直线CD与⊙O相切.连接OC,根据OA=OC,推出∠BAC=∠OCA,求出∠OCA=∠CAM,推出OC∥AM,求出OC⊥CD,根据切线的判定推出即可.
解答:解:直线CD与⊙O相切.
理由如下:连接OC.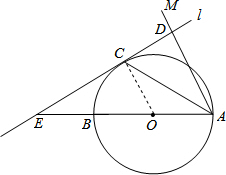
∵OA=OC,
∴∠BAC=∠OCA,
∵∠BAC=∠CAM,
∴∠OCA=∠CAM,
∴OC∥AM,
∵CD⊥AM,
∴OC⊥CD,
∵OC为半径,
∴直线CD与⊙O相切.
理由如下:连接OC.

∵OA=OC,
∴∠BAC=∠OCA,
∵∠BAC=∠CAM,
∴∠OCA=∠CAM,
∴OC∥AM,
∵CD⊥AM,
∴OC⊥CD,
∵OC为半径,
∴直线CD与⊙O相切.
点评:本题考查了切线的判定,要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
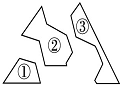 如图,某同学把一块三角形状的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样
如图,某同学把一块三角形状的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是带③去,依据是三角形的全等判定( )
| A、SAS | B、ASA |
| C、SSS | D、AAS |
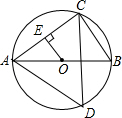 如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,BC=3.
如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,BC=3. 如图,已知线段a、b、c(a>b),用圆规和直尺画线段,使它等于a-b+2c.
如图,已知线段a、b、c(a>b),用圆规和直尺画线段,使它等于a-b+2c.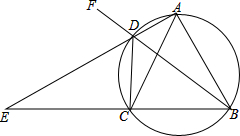 如图,四边形ABCD内接于圆,AD,BC的延长线交于点E,F是BD延长线上任意一点,若AB=AC.
如图,四边形ABCD内接于圆,AD,BC的延长线交于点E,F是BD延长线上任意一点,若AB=AC.