题目内容
9.如图1,在Rt△ABC中,∠ACB=90°,点P以每秒1cm的速度从点A出发,沿折线AC→CB运动,到点B停止.过点P作PD⊥AB于点D,PD的长y(cm)与点P的运动时间x(秒)的函数图象如图2所示.当点P运动4秒时,PD的长是( )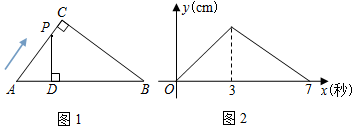
| A. | 2.4cm | B. | 1.5cm | C. | 1.8cm | D. | 1.2cm |
分析 根据图2可判断AC=3,BC=4,则可确定t=4时BP的值,利用sin∠B的值,可求出PD.
解答 解:由图2可得,AC=3,BC=4,
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
当t=4时,如图所示: ,
,
此时AC+CP=4,故BP=7-4=3,
∵sin∠B=$\frac{AC}{AB}$=$\frac{3}{5}$,
∴PD=BPsin∠B=3×$\frac{3}{5}$=$\frac{9}{5}$=1.8cm.
故选C.
点评 本题考查了动点问题的函数图象,解答本题的关键是根据图2得到AC、BC的长度,此题难度一般.

练习册系列答案
相关题目
19.四边形ABCD中,AC=BD,顺次连接ABCD各边中点得到的图形为( )
| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
17.下列运算,正确的是( )
| A. | 4a3-a2=3a | B. | a6÷a3=a2 | C. | a2•a3=a5 | D. | (-2a)2=-4a2 |
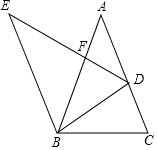 如图△EDB由△ABC绕点B逆时针旋转而来,D点落在AC上,DE交AB于点F,若AB=AC,DB=BF,则AF与BF的比值为$\frac{\sqrt{5}-1}{2}$.
如图△EDB由△ABC绕点B逆时针旋转而来,D点落在AC上,DE交AB于点F,若AB=AC,DB=BF,则AF与BF的比值为$\frac{\sqrt{5}-1}{2}$.