题目内容
11.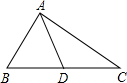 如图,在△ABC中,AD是BC边上的中线,若AB=3cm,AC=5cm,则AD的取值范围是1cm<AD<4cm.
如图,在△ABC中,AD是BC边上的中线,若AB=3cm,AC=5cm,则AD的取值范围是1cm<AD<4cm.
分析 延长AD到E,使DE=AD,连接BE,利用“边角边”证明△ACD和△EBD全等,根据全等三角形对应边相等可得BE=AC,再利用三角形的任意两边之和大于第三边,任意两边之差小于第三边求出AE的取值范围,然后求解即可.
解答 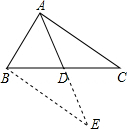 解:如图,延长AD到E,使DE=AD,连接BE,
解:如图,延长AD到E,使DE=AD,连接BE,
∵AD是BC边上的中线,
∴BD=CD,
在△ACD和△EBD中,$\left\{\begin{array}{l}{DE=AD}\\{∠ADC=∠EDB}\\{BD=CD}\end{array}\right.$,
∴△ACD≌△EBD(SAS),
∴BE=AC,
由三角形三边关系得,5-3<AE<5+3,
即2cm<AE<8cm,
∴1cm<AD<4cm.
故答案为:1cm<AD<4cm.
点评 本题考查了全等三角形的判定与性质,三角形的三边关系,“遇中线,加倍延”作辅助线构造出全等三角形是解题的关键,也是本题的难点.

练习册系列答案
相关题目
20.在春节到来之际,某童装推出系列活动,一位妈妈看好两件衣服,她想给孩子都买下来作为新年礼物,与店员商量希望都以60元的价格卖给她.销售员发现这样一件就会盈利25%,另一件就会亏损25%,如果这样卖出去,那么商店( )
| A. | 不盈不亏 | B. | 盈利50元 | C. | 盈利8元 | D. | 亏损8元 |
1.某商场卖出两部进价不同的手机,都卖了1200元,其中一部盈利20%,另一部亏损20%,在这次买卖中,这家商场( )
| A. | 赔了100元 | B. | 赚了100元 | C. | 不赔不赚 | D. | 赚了180元 |
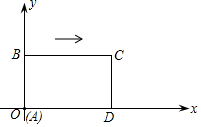 如图所示,在直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=5.若矩形以每秒2个单位长度沿x轴正方向作匀速运动,设运动时间为t(秒).
如图所示,在直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=5.若矩形以每秒2个单位长度沿x轴正方向作匀速运动,设运动时间为t(秒).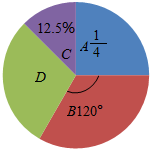 小琳对年级参加兴趣小组的同学进行调查,结果如图所示(每位同学只参加一类兴趣小组).其中A为参加艺术类兴趣小组的同学,B为参加体育竞技类兴趣小组的同学,C是参加科技类兴趣小组的同学,D为参加其他课外兴趣小组的同学.已知参加艺术类兴趣小组的同学有24人.问:
小琳对年级参加兴趣小组的同学进行调查,结果如图所示(每位同学只参加一类兴趣小组).其中A为参加艺术类兴趣小组的同学,B为参加体育竞技类兴趣小组的同学,C是参加科技类兴趣小组的同学,D为参加其他课外兴趣小组的同学.已知参加艺术类兴趣小组的同学有24人.问: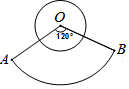 如图,已知圆O的周长与扇形OAB所对的弧长的比值为1,那么圆O的面积与扇形OAB的面积的比值为$\frac{1}{3}$.
如图,已知圆O的周长与扇形OAB所对的弧长的比值为1,那么圆O的面积与扇形OAB的面积的比值为$\frac{1}{3}$.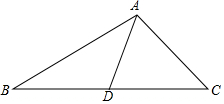 如图,在三角形ABC中,AD为中线,AB=4,AC=2,AD为整数,求AD的长.
如图,在三角形ABC中,AD为中线,AB=4,AC=2,AD为整数,求AD的长. 如图,在△ABC中,∠C=90°,∠A、∠B的平分线交于O,OD⊥AB于D.若AC=3,BC=4,AB=5,则AD=2.
如图,在△ABC中,∠C=90°,∠A、∠B的平分线交于O,OD⊥AB于D.若AC=3,BC=4,AB=5,则AD=2.