题目内容
2.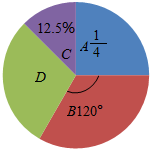 小琳对年级参加兴趣小组的同学进行调查,结果如图所示(每位同学只参加一类兴趣小组).其中A为参加艺术类兴趣小组的同学,B为参加体育竞技类兴趣小组的同学,C是参加科技类兴趣小组的同学,D为参加其他课外兴趣小组的同学.已知参加艺术类兴趣小组的同学有24人.问:
小琳对年级参加兴趣小组的同学进行调查,结果如图所示(每位同学只参加一类兴趣小组).其中A为参加艺术类兴趣小组的同学,B为参加体育竞技类兴趣小组的同学,C是参加科技类兴趣小组的同学,D为参加其他课外兴趣小组的同学.已知参加艺术类兴趣小组的同学有24人.问:(1)参与调查的同学共有多少人?
(2)参加体育竞技类和科技类兴趣小组的同学共占几分之几?
(3)参加其他兴趣小组的同学所占扇形的圆心角是多少度?
分析 (1)根据参加艺术类兴趣小组的同学共24人,占参与调查总人数的$\frac{1}{4}$,可得出总人数;
(2)先根据参加体育竞技类部分的圆心角除以圆周角360得到参加体育竞技类所占的百分比,加上科技类兴趣小组的同学所占的百分比,解答即可;
(3)分别求出AC两类所占圆心角的度数,进而可得出结论.
解答 解:(1)∵参加艺术类兴趣小组的同学共24人,占参与调查总人数的$\frac{1}{4}$,
∴参与调查的同学总人数=24÷$\frac{1}{4}$=96(人);
答:参与调查的同学共有96人.
(2)∵由图可知参加体育竞技类兴趣小组的同学所占的比例=$\frac{120}{360}$=$\frac{1}{3}$,
参加科技类兴趣小组的同学占12.5%=$\frac{1}{8}$,
∴加体育竞技类和科技类兴趣小组的同学共占总人数的比例=$\frac{1}{8}$+$\frac{1}{3}$=$\frac{11}{24}$.
答:参加体育竞技类和科技类兴趣小组的同学共占$\frac{11}{24}$;
③∵A类占总人数的$\frac{1}{4}$,
∴所占圆心角为90°.
∵C类占总人数的12.5%,
∴所占圆心角=12.5%×360°=45°,
∴D类所占圆心角=360°-90°-120°-45°=105°.
答:参加其他兴趣小组的同学所占扇形的圆心角是105°.
点评 本题考查的是扇形统计图,扇形统计图是用整个圆表示总数用圆内各个扇形的大小表示各部分数量占总数的百分数.通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.用整个圆的面积表示总数(单位1),用圆的扇形面积表示各部分占总数的百分数.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
1.设等腰三角形底角的度数x(单位:度)为自变量,顶角的度数y为因变量,则y与x的函数关系式为( )
| A. | y=180-2x(0<x<90) | B. | y=90-x(0≤x≤90) | C. | y=180-x(0<x<90) | D. | y=90-2x(0≤x≤90) |
2.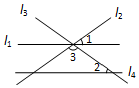 如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=∠2=36°,则∠3的度数为( )
如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=∠2=36°,则∠3的度数为( )
 如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=∠2=36°,则∠3的度数为( )
如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=∠2=36°,则∠3的度数为( )| A. | 60° | B. | 90° | C. | 108° | D. | 150° |
17.下列分数中不能化为有限小数的是( )
| A. | $\frac{7}{25}$ | B. | $\frac{7}{32}$ | C. | $\frac{3}{80}$ | D. | $\frac{5}{12}$ |
14.在下列分数中:不能化成有限小数的是( )
| A. | $\frac{4}{25}$ | B. | $\frac{9}{16}$ | C. | $\frac{3}{12}$ | D. | $\frac{1}{30}$ |
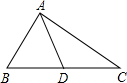 如图,在△ABC中,AD是BC边上的中线,若AB=3cm,AC=5cm,则AD的取值范围是1cm<AD<4cm.
如图,在△ABC中,AD是BC边上的中线,若AB=3cm,AC=5cm,则AD的取值范围是1cm<AD<4cm.