题目内容
3. 如图,在△ABC中,∠C=90°,∠A、∠B的平分线交于O,OD⊥AB于D.若AC=3,BC=4,AB=5,则AD=2.
如图,在△ABC中,∠C=90°,∠A、∠B的平分线交于O,OD⊥AB于D.若AC=3,BC=4,AB=5,则AD=2.
分析 根据三角形角平分线的交点到边的距离相等,再利用三角形面积公式解答即可.
解答  解:过O作OE⊥AC于E,OF⊥BC于F,
解:过O作OE⊥AC于E,OF⊥BC于F,
∵∠A、∠B的平分线交于O,OD⊥AB于D,
∴OD=OE=OF,
∵∠C=90°,
∴四边形ECFO是正方形,
∴OE=OF=CE=CF,
∵△ABC的面积=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•OD+$\frac{1}{2}$AC•OE+$\frac{1}{2}$BC•OF,
即$\frac{1}{2}$×3×4=$\frac{1}{2}$OE×(3+4+5),
解得:OE=1,
∴CE=OE=1,
∴AE=AC-CE=2,
在Rt△AEO与Rt△ADO中,$\left\{\begin{array}{l}{AO=AO}\\{OE=OD}\end{array}\right.$,
∴Rt△AEO≌Rt△ADO,
∴AD=AE=2,
故答案为:2.
点评 本题考查了角平分线的性质,全等三角形的判定和性质,正方形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
2.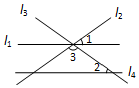 如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=∠2=36°,则∠3的度数为( )
如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=∠2=36°,则∠3的度数为( )
 如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=∠2=36°,则∠3的度数为( )
如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠1=∠2=36°,则∠3的度数为( )| A. | 60° | B. | 90° | C. | 108° | D. | 150° |
14.在下列分数中:不能化成有限小数的是( )
| A. | $\frac{4}{25}$ | B. | $\frac{9}{16}$ | C. | $\frac{3}{12}$ | D. | $\frac{1}{30}$ |
15. 小明在班里共有56名同学,他们给生日相同的小红与小亮过完生日后,对“多少人中必有2人生日相同”进行了讨论,下列说法中正确的是( )
小明在班里共有56名同学,他们给生日相同的小红与小亮过完生日后,对“多少人中必有2人生日相同”进行了讨论,下列说法中正确的是( )
 小明在班里共有56名同学,他们给生日相同的小红与小亮过完生日后,对“多少人中必有2人生日相同”进行了讨论,下列说法中正确的是( )
小明在班里共有56名同学,他们给生日相同的小红与小亮过完生日后,对“多少人中必有2人生日相同”进行了讨论,下列说法中正确的是( )| A. | 50人中必有2人的生日相同 | B. | 100人中必有2人的生日相同 | ||
| C. | 365人中必有2人的生日相同 | D. | 367人中必有2人的生日相同 |
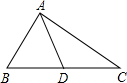 如图,在△ABC中,AD是BC边上的中线,若AB=3cm,AC=5cm,则AD的取值范围是1cm<AD<4cm.
如图,在△ABC中,AD是BC边上的中线,若AB=3cm,AC=5cm,则AD的取值范围是1cm<AD<4cm.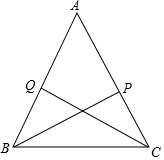 如图,CQ和BP是△ABC的角平分线,且BQ=CP,求证:AB=AC.
如图,CQ和BP是△ABC的角平分线,且BQ=CP,求证:AB=AC.