题目内容
4.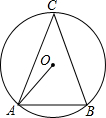 如图,⊙O是△ABC的外接圆,C是优弧AB上一点,设∠OAB=α,∠C=β.
如图,⊙O是△ABC的外接圆,C是优弧AB上一点,设∠OAB=α,∠C=β.(1)当β=36°时,求α的度数;
(2)猜想α与β之间的关系,并给予证明.
(3)若点C平分优弧AB,且BC2=3OA2,试求α的度数.
分析 (1)连接OB,根据同弧所对的圆周角是圆心角的一半和等腰三角形的性质解答即可;
(2)根据(1)的方法解答即可;
(3)过O作OE⊥AC于E,连接OC,证明AE=$\frac{\sqrt{3}}{2}$OA,得到△ABC为正三角形,得到答案.
解答 解:(1)连接OB,则OA=OB,
∴∠OAB=∠OBA,
∵∠C=36°,
∴∠AOB=72°,
∵∠OAB=$\frac{1}{2}$(180°-∠AOB)=54°,
即β=54°.
(2)α与β之间的关系是α+β=90°;
证明:∵∠OBA=∠OAB=α,
∴∠AOB=180°-2α,
∵∠AOB=2∠β,
∴180°-2α=2∠β,
∴α+β=90°.
(3)∵点C平分优弧AB
∴AC=BC
又∵BC2=3OA2,
∴AC=BC=$\sqrt{3}$OA,
过O作OE⊥AC于E,连接OC,
由垂径定理可知AE=$\frac{\sqrt{3}}{2}$OA,
∴∠AOE=60°,∠OAE=30°,
∴∠ABC=60°,
∴△ABC为正三角形,
则α=∠CAB-∠CAO=30°.
点评 本题考查的是三角形的外接圆、垂径定理和锐角三角函数的知识,综合性较强,需要学生灵活运用所学的知识,正确作出辅助线构造直角三角形进行解答.

练习册系列答案
相关题目
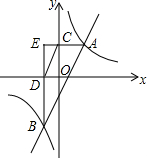 如图,反比例函数y=$\frac{k}{x}$(k>0)与一次函数y=ax-2(a>0)的图象都经过点A、B,过点A作AC⊥y轴与点C,过点B作BD⊥x轴于点D.
如图,反比例函数y=$\frac{k}{x}$(k>0)与一次函数y=ax-2(a>0)的图象都经过点A、B,过点A作AC⊥y轴与点C,过点B作BD⊥x轴于点D.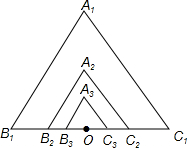 如图所示,由位似的正△A1B1C1,正△A2B2C2,正△A3B3C3,…正△AnBnCn组成的相似图形,其中第一个△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,A3是OA2的中点…An是OAn-1的中点,顶点B2,B3,…,Bn.C2,C3,…,Cn都在B1C1边上.
如图所示,由位似的正△A1B1C1,正△A2B2C2,正△A3B3C3,…正△AnBnCn组成的相似图形,其中第一个△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,A3是OA2的中点…An是OAn-1的中点,顶点B2,B3,…,Bn.C2,C3,…,Cn都在B1C1边上.