题目内容
16．
如图，方格纸中每个小正方形的边长都是单位1，△ABC的三个顶点都在格点上，结合所给的平面直角坐标系解答下列问题：（1）将△ABC向右平移3个单位长度，再向下平移2个单位长度，画出两次平移后的△A1B1C1；
（2）将△A1B1C1绕点（3，0）逆时针旋转90°，画出旋转后的图形；
（3）直接写出线段B1C1在变换过程中所扫过的面积．
分析 （1）根据图形平移的性质画出两次平移后的△A1B1C1即可；
（2）根据图形旋转的性质画出旋转后的△A2B2C2即可；
（3）根据勾股定理求出扇形的半径，由扇形的面积公式即可计算出线段B1C1旋转过程中扫过的面积．
解答 解：（1）如图所示，△A1B1C1即为所求；
（2）如图所示，的△A2B2C2即为所求；
（3）线段B1C1在变换过程中所扫过的面积=$\frac{1}{4}$（26π-1π）=$\frac{25}{4}$π．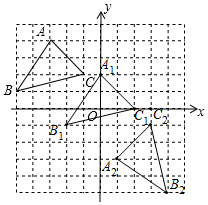
点评 本题主要考查了利用旋转、平移变换进行作图，以及扇形面积的计算，解决问题的关键是掌握扇形面积计算公式：设圆心角是n°，圆的半径为R的扇形面积为S，则 S扇形=$\frac{n}{360}$πR2．
练习册系列答案
智能训练练测考系列答案
相关题目
如图所示，在五边形ABCDE中，∠A=∠C=90°，试说明∠B=∠DEF+∠EDG．
5．有这样的一列数，第一个数为x1=-1，第二个数为x2=-3，从第三个数开始，每个数都等于它相邻两个数之和的一半（如：x2=$\frac{{x}_{1}+{x}_{3}}{2}$），则x2015等于（ ）
| A． | -2015 | B． | -4027 | C． | -4029 | D． | -4031 |
利用平面直角坐标系求抛物线y=x2-4x+3与坐标轴的交点围成的△ABC的周长和面积．抛物线上是否存在点D，使△ABD与△ABC面积相等，如果有，请写出D点坐标．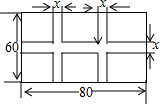
一块矩形耕地大小尺寸如图所示，要在这块地上沿东西方向挖一条水渠，沿南北方向挖两条水渠，水渠宽为xm，余下的可耕地面积为ym2．
如图，已知AB⊥BC，垂足为点B，AB⊥AD，垂足为点A，点E是CD的中点，说明：AE=BE．