题目内容
8. 如图,已知AB⊥BC,垂足为点B,AB⊥AD,垂足为点A,点E是CD的中点,说明:AE=BE.
如图,已知AB⊥BC,垂足为点B,AB⊥AD,垂足为点A,点E是CD的中点,说明:AE=BE.
分析 延长DA,BE交于点F,根据已知条件得到DF∥BC,根据平行线的性质得到∠F=∠EBC,推出△DEF≌△BCE,根据全等三角形的性质得到BE=EF,根据直角三角形的性质即可得到结论.
解答  解:延长DA,BE交于点F,
解:延长DA,BE交于点F,
∵AB⊥BC,AB⊥AD,
∴DF∥BC,
∴∠F=∠EBC,
∵点E是CD的中点,
∴DE=CE,
在△DEF与△BCE中,$\left\{\begin{array}{l}{∠F=∠EBC}\\{∠DEF=∠BEC}\\{DE=CE}\end{array}\right.$,
∴△DEF≌△BCE,
∴BE=EF,
∵BA⊥DF,
∴∠BAF=90°,
∴AE=BE=$\frac{1}{2}$BF.
点评 本题本题考查了平行线的判定,全等三角形的判定和性质,直角三角形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
17.下列各对量中,不具有相反意义的是( )
| A. | 胜3局与负4局 | B. | 收入3000元与支出2000元 | ||
| C. | 气温升高4℃与气温升高10℃ | D. | 转盘逆时针转3圈与顺时针转5圈 |
 如图,己知△ABC中,D点是BC的中点,BC切圆O于D,AB、AC与圆O相交于E、F,求证EF∥BC.
如图,己知△ABC中,D点是BC的中点,BC切圆O于D,AB、AC与圆O相交于E、F,求证EF∥BC. ,AC=3
,AC=3 ,BC=6,则⊙O的半径是__________________.
,BC=6,则⊙O的半径是__________________.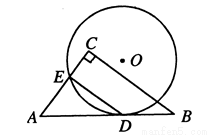
 如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题: 如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动,设运动时间为t s.
如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动,设运动时间为t s. 如图,已知二次函数y=-$\frac{1}{2}$x2+bx+c的图象经过(1,0),B(0,-6)两点,
如图,已知二次函数y=-$\frac{1}{2}$x2+bx+c的图象经过(1,0),B(0,-6)两点, △ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.
△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.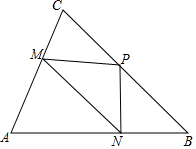 如图,在△ABC中,∠A=60°、∠B=45°、AB=4,点M、N、P分别在AC、AB、BC上运动,求△PMN周长的最小值.
如图,在△ABC中,∠A=60°、∠B=45°、AB=4,点M、N、P分别在AC、AB、BC上运动,求△PMN周长的最小值.