题目内容
14. 如图所示,在五边形ABCDE中,∠A=∠C=90°,试说明∠B=∠DEF+∠EDG.
如图所示,在五边形ABCDE中,∠A=∠C=90°,试说明∠B=∠DEF+∠EDG.
分析 利用五边形内角和定理和五边形外角定理进行解答.
解答 证明:五边形ABCDE内角和=3×180°=540°
∴∠B+∠AED+∠EDC=540°-90°-90°=360°,
∵∠AED+∠FED=180°,∠EDG+∠EDC=180°
∴∠AED+∠EDG+∠FED+∠EDC=360°
∴∠B=∠FED+∠EDG.
点评 本题考查了多边形内角与外角.此题比较简单,只要结合多边形的内角和公式与外角和的关系来寻求等量关系.

练习册系列答案
相关题目
4. 如图,四边形ABCD是⊙O的内接四边形,E在BC的延长线上,若∠A:∠B:∠D=4:3:3,则∠DCE的度数是( )
如图,四边形ABCD是⊙O的内接四边形,E在BC的延长线上,若∠A:∠B:∠D=4:3:3,则∠DCE的度数是( )
 如图,四边形ABCD是⊙O的内接四边形,E在BC的延长线上,若∠A:∠B:∠D=4:3:3,则∠DCE的度数是( )
如图,四边形ABCD是⊙O的内接四边形,E在BC的延长线上,若∠A:∠B:∠D=4:3:3,则∠DCE的度数是( )| A. | 100° | B. | 105° | C. | 110° | D. | 120° |
2.在梯形ABCD中,AD∥BC,AC与BD相交于点O,如果AD:BC=1:3,那么下列结论中正确的是( )
| A. | S△COD=S△AOD | B. | S△ABC=S△ACD | C. | S△BOC=3•S△AOD | D. | S△BOC=9•S△AOD |
9.汽车从甲地匀速向乙地行驶,汽车离乙地的距离s与行驶时间t之间的关系如下表所示
(1)根据表中数据,你能知道甲地和乙地相距多远吗?
(2)写出汽车离乙地的距离s与行驶时间t的关系式;
(3)当t=6.5h时,求汽车离乙地的距离;
(4)如果这辆汽车上午8:00从甲地出发,途中休息20分钟,按照表中的行驶速度,几点钟可以到达乙地?
| 行驶时间(h) | 0 | 1 | 2 | 3 | 4 | 5 |
| 距乙地距离(km) | 800 | 720 | 640 | 560 | 480 | 400 |
(2)写出汽车离乙地的距离s与行驶时间t的关系式;
(3)当t=6.5h时,求汽车离乙地的距离;
(4)如果这辆汽车上午8:00从甲地出发,途中休息20分钟,按照表中的行驶速度,几点钟可以到达乙地?
17.下列各对量中,不具有相反意义的是( )
| A. | 胜3局与负4局 | B. | 收入3000元与支出2000元 | ||
| C. | 气温升高4℃与气温升高10℃ | D. | 转盘逆时针转3圈与顺时针转5圈 |
 如图,己知△ABC中,D点是BC的中点,BC切圆O于D,AB、AC与圆O相交于E、F,求证EF∥BC.
如图,己知△ABC中,D点是BC的中点,BC切圆O于D,AB、AC与圆O相交于E、F,求证EF∥BC. ,
,  ,
,  )
)
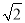 ,AC=3
,AC=3 ,BC=6,则⊙O的半径是__________________.
,BC=6,则⊙O的半径是__________________.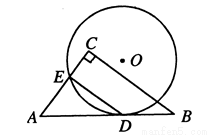
 如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题: