题目内容
11. 利用平面直角坐标系求抛物线y=x2-4x+3与坐标轴的交点围成的△ABC的周长和面积.抛物线上是否存在点D,使△ABD与△ABC面积相等,如果有,请写出D点坐标.
利用平面直角坐标系求抛物线y=x2-4x+3与坐标轴的交点围成的△ABC的周长和面积.抛物线上是否存在点D,使△ABD与△ABC面积相等,如果有,请写出D点坐标.
分析 求出A、B、C三点的坐标后,然后即可求出AB、AC、BC的长度;由于△ABD与△ABC面积相等,即它们的高也相等.
解答 解:令y=0代入y=x2-4x+3,
∴0=x2-4x+3,
∴x=1或x=3,
∴A(1,0),B(3,0),
∴AB=2,OB=3,OA=1,
令x=0代入y=x2-4x+3,
∴y=3,
∴C(0,3),
∴由勾股定理可求得:AC=$\sqrt{10}$,BC=3$\sqrt{2}$,
∴△ABC的周长为:AC+AB+BC=2+$\sqrt{10}$+3$\sqrt{2}$,
△ABC的面积为:$\frac{1}{2}$AB•OC=$\frac{1}{2}$×2×3=3,
设△ABD的边AB上的高为h,
∴h=3,
∴即D的纵坐标为±3,
设D(x,y),
当y=3时,
此时3=x2-4x+3,
解得x=0(舍去)或x=4,
∴当y=-3时,
∴此时-3=x2-4x+3,
∴△<0,
∴方程无解,
综上所述,D的坐标为(4,3)
点评 本题考查二次函数综合问题,涉及勾股定理,三角形面积公式,一元二次方程等知识,题型较为综合.

练习册系列答案
相关题目
9.汽车从甲地匀速向乙地行驶,汽车离乙地的距离s与行驶时间t之间的关系如下表所示
(1)根据表中数据,你能知道甲地和乙地相距多远吗?
(2)写出汽车离乙地的距离s与行驶时间t的关系式;
(3)当t=6.5h时,求汽车离乙地的距离;
(4)如果这辆汽车上午8:00从甲地出发,途中休息20分钟,按照表中的行驶速度,几点钟可以到达乙地?
| 行驶时间(h) | 0 | 1 | 2 | 3 | 4 | 5 |
| 距乙地距离(km) | 800 | 720 | 640 | 560 | 480 | 400 |
(2)写出汽车离乙地的距离s与行驶时间t的关系式;
(3)当t=6.5h时,求汽车离乙地的距离;
(4)如果这辆汽车上午8:00从甲地出发,途中休息20分钟,按照表中的行驶速度,几点钟可以到达乙地?
1.已知:$\frac{x}{y}$=$\frac{2}{3}$,则下列结论一定正确的是( )
| A. | x=2,y=3 | B. | 2x=3y | C. | $\frac{x+y}{y}=\frac{5}{3}$ | D. | $\frac{x+2}{y+3}=\frac{2}{3}$ |
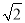 ,AC=3
,AC=3 ,BC=6,则⊙O的半径是__________________.
,BC=6,则⊙O的半径是__________________.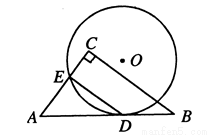
 如图,直线AB、CD相交于点O,OE⊥AB,∠EOD=20°,∠AOC=70°.
如图,直线AB、CD相交于点O,OE⊥AB,∠EOD=20°,∠AOC=70°. 如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题: 如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动,设运动时间为t s.
如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动,设运动时间为t s. △ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.
△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.