题目内容
17. 已知:如图,△ABC中,AD⊥BC于D,E是AD上一点,BE的延长线交AC于F,若BD=AD,DE=DC.
已知:如图,△ABC中,AD⊥BC于D,E是AD上一点,BE的延长线交AC于F,若BD=AD,DE=DC.①求证:△BED≌△ACD.
②求证:BF⊥AC.
分析 ①求出∠BDE=∠ADC=90°,根据SAS推出两三角形全等即可;
②根据全等三角形的性质得出∠CAD=∠DBE,根据三角形内角和定理求出∠DBE+∠BED=90°,求出∠AEF+∠CAD=90°,根据三角形内角和定理求出∠AFE=90°,即可得出答案.
解答 证明:①∵AD⊥BC,
∴∠BDE=∠ADC=90°,
在△BED和△ACD中
$\left\{\begin{array}{l}{DB=DA}\\{∠BDE=∠ADC}\\{DE=DC}\end{array}\right.$
∴△BED≌△ACD(SAS);
②∵△BED≌△ACD,
∴∠CAD=∠DBE,
∵∠BDE=90°,
∴∠DBE+∠BED=90°,
∵∠BED=∠AEF,∠DBE=∠CAD,
∴∠AEF+∠CAD=90°,
∴∠AFE=180°-90°=90°,
∴BF⊥AC.
点评 本题考查了全等三角形的性质和判定,三角形内角和定理的应用,能推出△BED≌△ACD是解此题的关键.

练习册系列答案
相关题目
8.若2m=3,2n=5,则2m+2n=( )
| A. | 15 | B. | 30 | C. | 45 | D. | 75 |
5.在0,-9,-|-3|,-(-5),4,6.8中,正整数的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
12.若α,β是一元二次方程x2+2x-6=0的两根,则α+β的值是( )
| A. | -6 | B. | 6 | C. | -2 | D. | 2 |
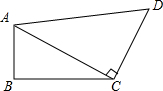 如图是一块四边形草坪ABCD,已知∠ACD=90°,AB=3m,BC=CD=4m,AD=$\sqrt{41}$m,求草坪的面积.
如图是一块四边形草坪ABCD,已知∠ACD=90°,AB=3m,BC=CD=4m,AD=$\sqrt{41}$m,求草坪的面积.