题目内容
6.(1)若关于x的二次三项式x2+px+12能在整数范围内因式分解为(x+a)(x+b),其中a,b均为整数,请写出所有符合条件的p的值,并将相应的多项式因式分解.(2)试分解因式x2+x-12.
分析 (1)利用十字相乘法的方法判断确定出所有p的值即可;
(2)原式利用十字相乘法分解即可.
解答 解:(1)根据题意得:x2+px+12=(x+1)(x+12)=(x+2)(x+6)=(x+3)(x+4)=(x-1)(x-12)=(x-2)(x-6)=(x-3)(x-4),
则所有p的值为13,8,7,-13,-8,-7;
(2)原式=(x-3)(x+4).
点评 此题考查了因式分解-十字相乘法,熟练掌握十字相乘法是解本题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
11.点(0,0)是( )
| A. | 抛物线y=x2的最低点 | |
| B. | 抛物线y=x2的最高点 | |
| C. | 抛物线y=-x2的最低点 | |
| D. | 抛物线y=x2和抛物线y=-x2的最低点 |
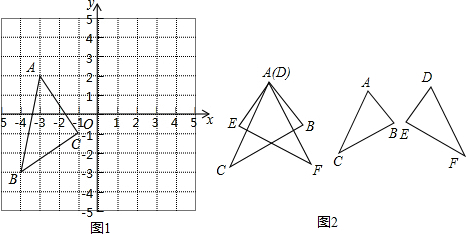
 已知:如图,△ABC中,AD⊥BC于D,E是AD上一点,BE的延长线交AC于F,若BD=AD,DE=DC.
已知:如图,△ABC中,AD⊥BC于D,E是AD上一点,BE的延长线交AC于F,若BD=AD,DE=DC. 如图.要判定AB∥CD,需要哪些条件?根据是什么?
如图.要判定AB∥CD,需要哪些条件?根据是什么?