题目内容
9．计算：（1+$\frac{1}{2}$）（1+$\frac{1}{4}$）（1+$\frac{1}{16}$）（1+$\frac{1}{256}$）…（1+$\frac{1}{{2}^{2n}}$）分析 把原式化成2（1-$\frac{1}{2}$）（1+$\frac{1}{2}$）（1+$\frac{1}{4}$）（1+$\frac{1}{16}$）（1+$\frac{1}{256}$）…（1+$\frac{1}{{2}^{2n}}$），然后根据平方差公式计算即可．
解答 解：原式=2（1-$\frac{1}{2}$）（1+$\frac{1}{2}$）（1+$\frac{1}{4}$）（1+$\frac{1}{16}$）（1+$\frac{1}{256}$）…（1+$\frac{1}{{2}^{2n}}$）
=2（1-$\frac{1}{{2}^{4n}}$）
=2-$\frac{1}{{2}^{4n-1}}$．
点评 本题考查了有理数的混合运算，熟练掌握和运用平方差公式是解题的关键．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
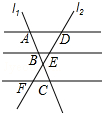如图，AD∥BE∥CF，直线l1，l2与这三条平行线分别交于点A，B，C和点D，E，F，$\frac{AB}{BC}$=$\frac{2}{3}$，DE=6，则DF的值为（ ）
已知：如图，△ABC中，AD⊥BC于D，E是AD上一点，BE的延长线交AC于F，若BD=AD，DE=DC．
一几何体是由若干个相同的小立方块搭成的，它的主视图和左视图相同，且如图所示，则搭该几何体的小立方块最多几块？最少几块？