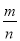��Ŀ����
��ͼ,��֪��B=��ACD,��ACB=��D=90��,AC�ǡ�ABC�͡�ACD�Ĺ�����,���ԾͿ����ж���ABC�ա�ACD.����Ϊ����˵����ȷ��?�������ȷ,��˵������.
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д����йط����Ϥ��������ũ���Ѿ�ʵ����ũ�����ͺ���ҽ�Ʊ����ƶȣ�����ҽ����ũ����ڹ涨��ҽԺ��ҽ�����涨����������ҽ�Ʒ��ã��±���ҽ�Ʒ��ñ����ı���
ҽ�Ʒ��÷�Χ | ���� | סԺ | ||
0��5000Ԫ | 5001��20000Ԫ | 20000Ԫ���� | ||
ÿ�걨�������� | 30% | 30% | 40% | 50% |
(˵����סԺҽ�Ʒ��õı����ֶμ��㣮�磺ij��סԺҽ�Ʒ��ù�30000Ԫ����5000Ԫ��30%������15000Ԫ��40%���������µ�10000Ԫ��50%�����������漰��ҽ�ƷѾ�ָ����������ҽ�Ʒ�)��
(1)ijũ��2016���������������ҽ�Ʒ�180Ԫ����������һ��������ҽ�Ʒ��ù�________Ԫ��
(2)��ijũ��һ����סԺ��ʵ��ҽ�Ʒ���ΪxԪ(5001��x��20000)�����������Ľ��ΪyԪ�������y��x�Ĺ�ϵʽ��
(3)��ijũ��һ���ڱ����Ը�סԺҽ�Ʒ�17000Ԫ(�Ը�ҽ�Ʒѣ�ʵ��ҽ�Ʒѣ����������Ľ��)�����ũ����ʵ��ҽ�Ʒ��ù�����Ԫ��
(1)600(2)y��0.4x��500(3) x��29000Ԫ �������������������1���������������ҽ�Ʒ�180Ԫ�� 30%x=180������ɣ� ��2������ͼ������x��ȡֵ��Χ�ó�y��x�ĺ�����ϵ���ɣ� ��3����ʵ��ҽ�Ʒѳ���20000��������ϵΪ��5000����1-30%��+15000����1-40%��+����20000��ҽ�Ʒѡ���1-50%��=17000���������ֵ������㼴...ij�̳�������һ����������ת����ת��,���涨:�˿���10Ԫ���Ͼ��ܻ��һ��ת��ת�̵Ļ���,��ת��ֹͣʱ,ָ��������һ����Ϳ��Ի����Ӧ�Ľ�Ʒ(��ͼ��ʾ).�±��ǻ�����е�һ��ͳ������:
ת��ת�� �Ĵ���n | 100 | 150 | 200 | 500 | 800 | 1 000 |
���ڡ�Ǧ�ʡ� ����Ĵ���m | 68 | 111 | 136 | 345 | 564 | 701 |
���ڡ�Ǧ�ʡ� �����Ƶ�� |
(1)���㲢��ɱ���.
(2)�����,��n�ܴ�ʱ,���ڡ�Ǧ�ʡ������Ƶ�ʽ���ӽ�����?
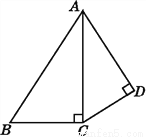
(3)������ȥת����ת��һ��,�������ֽ�Ʒ�Ļ����?
(4)�ڸ�ת����,��ʾ��Ǧ�ʡ���������ε�Բ�Ľ�Լ�Ƕ���?
 ��1��0.68��0.74��0.68��0.69��0.705��0.701����2��0.7����3��Ǧ�ʣ���4��252��.
����������������1������Ƶ�ʵ��㷨��Ƶ��=Ƶ�������ɵø���Ƶ�ʣ��ݴ���ռ��ɣ�
��2������3������Ƶ�ʵĶ��壬�ɵõ�n�ܴ�ʱ��Ƶ�ʽ���ӽ�����ʽ��н��
��4����������ͼ�У�ÿ����ռ����İٷֱȵ��ڸò�������Ӧ������Բ�ĽǵĶ�����360��ıȼ��㼴��.
�����...
��1��0.68��0.74��0.68��0.69��0.705��0.701����2��0.7����3��Ǧ�ʣ���4��252��.
����������������1������Ƶ�ʵ��㷨��Ƶ��=Ƶ�������ɵø���Ƶ�ʣ��ݴ���ռ��ɣ�
��2������3������Ƶ�ʵĶ��壬�ɵõ�n�ܴ�ʱ��Ƶ�ʽ���ӽ�����ʽ��н��
��4����������ͼ�У�ÿ����ռ����İٷֱȵ��ڸò�������Ӧ������Բ�ĽǵĶ�����360��ıȼ��㼴��.
�����... 

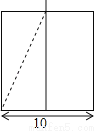
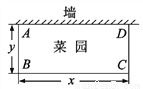
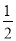 x��12(0��x��24)
x��12(0��x��24)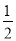 x��12(0��x��24)
x��12(0��x��24)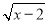 ���Ա���x��ȡֵ��Χ�ǣ� ��
���Ա���x��ȡֵ��Χ�ǣ� ��