题目内容
8. 如图,在?ABCD中,点E在线段AC上,BE=DE,∠1=∠2.
如图,在?ABCD中,点E在线段AC上,BE=DE,∠1=∠2.(1)若∠3=70°,求∠2度数;
(2)若AB=2BE-1,tan∠3=3tan∠1,求BE的长度.
分析 (1)由平行四边形和已知条件得出∠1=∠4,证出DE=CE,由三角形的外角性质求出∠2=35°即可;
(2)连接BD,交AC于O,由平行四边形的性质得出OB=OD,CD=AB=2BE-1,由等腰三角形的性质得出BD⊥AC,由tan∠3=3tan∠1=3tan∠4得出OC=3OE,因此DE=CE=2OE,求出∠ODE=30°,得出OD=$\sqrt{3}$OE,∠3=60°,∠4=30°,由含30°角的直角三角形的性质得出CD=2OD,设BE=DE=CE=x,则OD=$\frac{\sqrt{3}}{2}$x,CD=2x-1,得出方程,解方程即可.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠2=∠4,
∵∠1=∠2,
∴∠1=∠4,
∴DE=CE,
∵∠3=∠1+∠4=70°,
∴∠2=35°;
(2)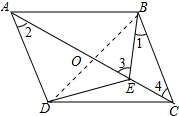 连接BD,交AC于O,如图所示:
连接BD,交AC于O,如图所示:
∵四边形ABCD是平行四边形,
∴OB=OD,CD=AB=2BE-1,
∵BE=DE,
∴BD⊥AC,
∵tan∠3=3tan∠1=3tan∠4,
∴$\frac{OD}{OE}=3×\frac{OD}{OC}$,
∴OC=3OE,
∴DE=CE=2OE,
∴∠ODE=30°,
∴OD=$\sqrt{3}$OE,∠3=60°,
∴∠4=30°,
∴CD=2OD,
设BE=DE=CE=x,则OD=$\frac{\sqrt{3}}{2}$x,CD=2x-1,
∴2x-1=2×$\frac{\sqrt{3}}{2}$x,
解得:x=2+$\sqrt{3}$,
∴BE=2+$\sqrt{3}$.
点评 本题考查了平行四边形的性质、等腰三角形的性质、解直角三角形等知识;熟练掌握平行四边形的性质,证明BD⊥AC是解决问题(2)的关键.

练习册系列答案
相关题目
18.若关于x的不等式组$\left\{\begin{array}{l}{x<2(x-a)}\\{x-1≤\frac{2}{3}x}\end{array}\right.$恰有3个整数解,则a的取值范围是( )
| A. | 0≤a<$\frac{1}{2}$ | B. | 0≤a<1 | C. | -$\frac{1}{2}$<a≤0 | D. | -1≤a<0 |
17. 如图,点P是△ABC内一点,且PD=PE=PF,则点P是( )
如图,点P是△ABC内一点,且PD=PE=PF,则点P是( )
 如图,点P是△ABC内一点,且PD=PE=PF,则点P是( )
如图,点P是△ABC内一点,且PD=PE=PF,则点P是( )| A. | △ABC三边垂直平分线的交点 | B. | △ABC三条角平分线的交点 | ||
| C. | △ABC三条高所在直线的交点 | D. | △ABC三条中线的交点 |
18.下列图形表示y是x函数图象的个数是( )

| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
 如图,从一个大正方形中截去面积为15cm2和24cm2的两个小正方形后剩余部分(阴影部分)的面积为12$\sqrt{10}$cm2.
如图,从一个大正方形中截去面积为15cm2和24cm2的两个小正方形后剩余部分(阴影部分)的面积为12$\sqrt{10}$cm2.
