题目内容
7.化简:$\frac{1}{1+x}$+$\frac{2}{1{+x}^{2}}$+$\frac{4}{1{+x}^{4}}$+$\frac{8}{1{+x}^{8}}$+$\frac{16}{1{+x}^{16}}$.分析 原式变形后,两项两项通分并利用同分母分式的加法法则计算,即可得到结果.
解答 解:原式=$\frac{1}{1-x}$+$\frac{1}{1+x}$+$\frac{2}{1+{x}^{2}}$+$\frac{4}{1+{x}^{4}}$+$\frac{8}{1+{x}^{8}}$+$\frac{16}{1+{x}^{16}}$-$\frac{1}{1-x}$
=$\frac{2}{1-{x}^{2}}$+$\frac{2}{1+{x}^{2}}$+$\frac{4}{1+{x}^{4}}$+$\frac{8}{1+{x}^{8}}$+$\frac{16}{1+{x}^{16}}$-$\frac{1}{x-1}$
=$\frac{4}{1-{x}^{4}}$+$\frac{4}{1+{x}^{4}}$+$\frac{8}{1+{x}^{8}}$+$\frac{16}{1+{x}^{16}}$-$\frac{1}{1-x}$
=$\frac{8}{1-{x}^{8}}$+$\frac{8}{1+{x}^{8}}$+$\frac{16}{1+{x}^{16}}$-$\frac{1}{1-x}$
=$\frac{16}{1-{x}^{16}}$+$\frac{16}{1+{x}^{16}}$-$\frac{1}{1-x}$
=$\frac{32}{1-{x}^{32}}$-$\frac{1}{1-x}$
=$\frac{32-32x-1+{x}^{32}}{(1-{x}^{32})(1-x)}$.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
12.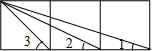 如图,是三个正方形拼成的一个长方形,则∠1+∠2+∠3=( )
如图,是三个正方形拼成的一个长方形,则∠1+∠2+∠3=( )
 如图,是三个正方形拼成的一个长方形,则∠1+∠2+∠3=( )
如图,是三个正方形拼成的一个长方形,则∠1+∠2+∠3=( )| A. | 60° | B. | 75° | C. | 90° | D. | 105° |
17.把方程x2-6x+3=0化成(x-m)2=n的形式,则m、n的值是( )
| A. | 3,12 | B. | -3,12 | C. | 3,6 | D. | -3,6 |