题目内容
我们知道：
=
-
，
=
-
，
=
-
，
那么
+
+
+…+
（其中a=
）的值为（ ）
| 1 |
| 1×2 |
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
那么
| a |
| 1×2 |
| a |
| 2×3 |
| a |
| 3×4 |
| a |
| 2014×2015 |
| 2015 |
| 2014 |
| A、2014 | B、2015 |
| C、1 | D、2 |
考点：代数式求值,有理数的混合运算
专题：规律型
分析：首先将
+
+
+…+
变形为：a（
+
+
+…+
），然后根据已知再将括号内的列项求和，最后将a=
代入即可．
| a |
| 1×2 |
| a |
| 2×3 |
| a |
| 3×4 |
| a |
| 2014×2015 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2014×2015 |
| 2015 |
| 2014 |
解答：解：
+
+
+…+
=a（
+
+
+…+
），
=a（ 1-
+
-
+
-
+…+
-
）
=a×（1-
）
=
×
=1．
故选：C．
| a |
| 1×2 |
| a |
| 2×3 |
| a |
| 3×4 |
| a |
| 2014×2015 |
=a（
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2014×2015 |
=a（ 1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2014 |
| 1 |
| 2015 |
=a×（1-
| 1 |
| 2015 |
=
| 2015 |
| 2014 |
| 2014 |
| 2015 |
=1．
故选：C．
点评：此题考查了代数式求值，解题的关键是：将
+
+
+…+
变形为：a（
+
+
+…+
），然后根据已知再将括号内的列项求和．
| a |
| 1×2 |
| a |
| 2×3 |
| a |
| 3×4 |
| a |
| 2014×2015 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2014×2015 |
练习册系列答案
相关题目
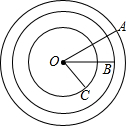如图所示，以点O为圆心的三个同心圆，最大圆的面积为75π cm2，如果以点O为圆心的两个小圆把大圆O的面积三等分．