题目内容
20.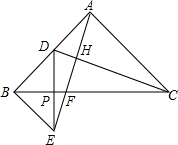 如图,在Rt△ABC中,∠BAC=90°,∠ACB=45°,点D是AB中点,AF⊥CD于点H,交BC于点F,BE∥AC交AF的延长线于点E,给出下列结论:①∠BAE=∠ACD,②△ADC≌△BEA,③AC=AF,④∠BDE=∠EDC,⑤BC⊥DE.上述结论正确的序号是( )
如图,在Rt△ABC中,∠BAC=90°,∠ACB=45°,点D是AB中点,AF⊥CD于点H,交BC于点F,BE∥AC交AF的延长线于点E,给出下列结论:①∠BAE=∠ACD,②△ADC≌△BEA,③AC=AF,④∠BDE=∠EDC,⑤BC⊥DE.上述结论正确的序号是( )| A. | ①②⑤ | B. | ②④⑤ | C. | ①②④ | D. | ①②③ |
分析 由∠BAE+∠FAC=90°,∠ACD+∠FAC=90°,得出∠BAE=∠ACD,①正确;由ASA证明△ADC≌△BEA,②正确;由AC=AB>AF,得出③不正确;由全等三角形的性质得出AD=BE,由AD=BD,得出BE=BD,∠BDE=45°≠∠EDC,④不正确;由等腰直角三角形的三线合一性质得出⑤正确;即可得出结论.
解答 解:∵∠BAC=90°,∠ACB=45°,
∴△ABC是等腰直角三角形,∠BAE+∠FAC=90°,
∴AB=AC,∠CBA=∠ACB=45°,
∵AF⊥CD,
∴∠AHC=90°,
∴∠ACD+∠FAC=90°,
∴∠BAE=∠ACD,①正确;
∵BE∥AC,
∴∠ABE+∠BAC=180°,
∴∠ABE=90°,
在△ADC和△BEA中,
$\left\{\begin{array}{l}{∠CAD=∠ABE=90°}&{\;}\\{AC=AB}&{\;}\\{∠ACD=∠BAE}&{\;}\end{array}\right.$,
∴△ADC≌△BEA(ASA),②正确;
∵AC=AB>AF,
∴③不正确;
∵△ADC≌△BEA,
∴AD=BE,
∵点D是AB中点,
∴AD=BD,
∴BE=BD,
∴∠BDE=45°≠∠EDC,④不正确;
∵∠ABE=90°,BE=BD,∠CBA=45°,
∴∠EBP=45°,
即BP平分∠ABE,
∴BP⊥DE,
即BC⊥DE,⑤正确.
故选:A.
点评 本题考查了全等三角形的判定与性质、等腰直角三角形的判定与性质、等腰三角形的性质、平行线的性质等知识;本题综合性强,有一定难度,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
10.已知反比例函数的图象经过点(1,-8),则它的图象一定也经过( )
| A. | (-2,-4) | B. | (-2,4) | C. | (-1,-8) | D. | (1,8) |
11. 如图几何体的俯视图是( )
如图几何体的俯视图是( )
 如图几何体的俯视图是( )
如图几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
 如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=-2x+2的图象.
如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=-2x+2的图象.