题目内容
20.下列命题中,假命题有( )①两点之间线段最短;②到角的两边距离相等的点在角的平分线上;
③过一点有且只有一条直线与已知直线平行;④垂直于同一直线的两条直线平行;
⑤若⊙O的弦AB,CD交于点P,则PA•PB=PC•PD.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 根据线段的性质公理判断①;
根据角平分线的性质判断②;
根据垂线的性质、平行公理的推论判断③④;
连接AC、DB,根据同弧所对的圆周角相等,证出△ACP∽△DBP,然后根据相似三角形的性质得出结论.依此判断⑤.
解答 解:①两点之间线段最短,说法正确,不是假命题;
②到角的两边距离相等的点在角的平分线上,说法正确,不是假命题;
③过直线外一点有且只有一条直线与已知直线平行,原来的说法错误,是假命题;
④在同一平面内,垂直于同一直线的两条直线平行,原来的说法错误,是假命题;
⑤ 如图,连接AC、BD.
如图,连接AC、BD.
∵∠A=∠D,∠C=∠B,
∴△ACP∽△DBP,
∴$\frac{PA}{PD}$=$\frac{PC}{PB}$,
∴PA•PB=PC•PD,
故若⊙O的弦AB,CD交于点P,则PA•PB=PC•PD的说法正确,不是假命题.
故选:C.
点评 本题考查了线段的性质公理,角平分线的性质,垂线的性质,平行公理的推论,点相交弦定理,是基础知识,需熟练掌握.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
11. 如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠2=65°,则∠1的度数是( )
如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠2=65°,则∠1的度数是( )
 如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠2=65°,则∠1的度数是( )
如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠2=65°,则∠1的度数是( )| A. | 65° | B. | 25° | C. | 35° | D. | 50° |
18.运用乘法公式计算(x+2y)(x-2y)的结果是( )
| A. | x2-4xy+4y2 | B. | x2+4xy+4y2 | C. | x2-4y2 | D. | x2+4y2 |
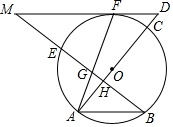 如图,AC是⊙O的直径,弦BE⊥AC于H,F为⊙O上的一点,过F的直线与AC延长线交于点D,与BE的延长线交于点M,连接AF交BM于G,且MF=MG.
如图,AC是⊙O的直径,弦BE⊥AC于H,F为⊙O上的一点,过F的直线与AC延长线交于点D,与BE的延长线交于点M,连接AF交BM于G,且MF=MG.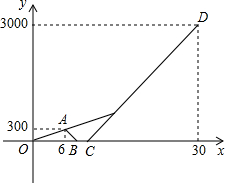 为营造书香家庭,周末小亮和姐姐一起从家出发去图书馆借书,走了6分钟忘带借书证,小亮立即骑路边共享单车返回家中取借书证,姐姐以原来的速度继续向前行走,小亮取到借书证后骑单车原路原速前往图书馆,小亮追上姐姐后用单车带着姐姐一起前往图书馆.已知单车的速度是步行速度的3倍,如图是小亮和姐姐距家的路程y(米)与出发的时间x(分钟)的函数图象,根据图象解答下列问题:
为营造书香家庭,周末小亮和姐姐一起从家出发去图书馆借书,走了6分钟忘带借书证,小亮立即骑路边共享单车返回家中取借书证,姐姐以原来的速度继续向前行走,小亮取到借书证后骑单车原路原速前往图书馆,小亮追上姐姐后用单车带着姐姐一起前往图书馆.已知单车的速度是步行速度的3倍,如图是小亮和姐姐距家的路程y(米)与出发的时间x(分钟)的函数图象,根据图象解答下列问题: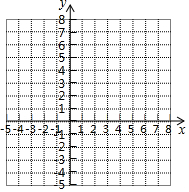 直线l的解析式为y=-2x+2,分别交x轴、y轴于点A,B.
直线l的解析式为y=-2x+2,分别交x轴、y轴于点A,B.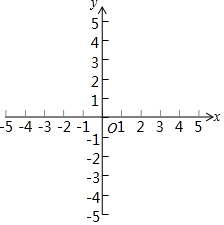 在平面直角坐标系xOy中,抛物线y=ax2+bx+2过点A(-2,0),B(2,2),与y轴交于点C.
在平面直角坐标系xOy中,抛物线y=ax2+bx+2过点A(-2,0),B(2,2),与y轴交于点C.