题目内容
8.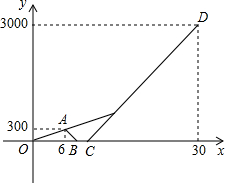 为营造书香家庭,周末小亮和姐姐一起从家出发去图书馆借书,走了6分钟忘带借书证,小亮立即骑路边共享单车返回家中取借书证,姐姐以原来的速度继续向前行走,小亮取到借书证后骑单车原路原速前往图书馆,小亮追上姐姐后用单车带着姐姐一起前往图书馆.已知单车的速度是步行速度的3倍,如图是小亮和姐姐距家的路程y(米)与出发的时间x(分钟)的函数图象,根据图象解答下列问题:
为营造书香家庭,周末小亮和姐姐一起从家出发去图书馆借书,走了6分钟忘带借书证,小亮立即骑路边共享单车返回家中取借书证,姐姐以原来的速度继续向前行走,小亮取到借书证后骑单车原路原速前往图书馆,小亮追上姐姐后用单车带着姐姐一起前往图书馆.已知单车的速度是步行速度的3倍,如图是小亮和姐姐距家的路程y(米)与出发的时间x(分钟)的函数图象,根据图象解答下列问题:(1)小亮在家停留了2分钟.
(2)求小亮骑单车从家出发去图书馆时距家的路程y(米)与出发时间x(分钟)之间的函数关系式.
(3)若小亮和姐姐到图书馆的实际时间为m分钟,原计划步行到达图书馆的时间为n分钟,则n-m=30分钟.
分析 (1)根据路程与速度、时间的关系,首先求出C、B两点的坐标,即可解决问题;
(2)根据C、D两点坐标,利用待定系数法即可解决问题;
(3)求出原计划步行到达图书馆的时间为n,即可解决问题.
解答 解:(1)步行速度:300÷6=50m/min,单车速度:3×50=150m/min,单车时间:3000÷150=20min,30-20=10,
∴C(10,0),
∴A到B是时间=$\frac{300}{150}$=2min,
∴B(8,0),
∴BC=2,
∴小亮在家停留了2分钟.
故答案为2.
(2)设y=kx+b,过C、D(30,3000),
∴$\left\{\begin{array}{l}0=10k+b\\ 3000=30k+b\end{array}$,解得$\left\{\begin{array}{l}k=150\\ b=-1500\end{array}$,
∴y=150x-1500(10≤x≤30)
(3)原计划步行到达图书馆的时间为n分钟,n=$\frac{3000}{50}$=60
n-m=60-30=30分钟,
故答案为30.
点评 本题考查一次函数的应用、路程、速度、时间之间的关系等知识,解题的关键是理解题意,读懂图象信息,灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
19.下列从左到右的变形是因式分解的是( )
| A. | ab-b=b(a-1) | B. | (m+n)(m-n)=m2-n2 | C. | -10x-10=-10(x-1) | D. | x2-2x+1=x(x-2)+1 |
16.根据分式的基本性质,分式$\frac{-a}{a-b}$可以变形为( )
| A. | $\frac{a}{-a+b}$ | B. | $\frac{a}{a+b}$ | C. | -$\frac{-a}{a-b}$ | D. | -$\frac{a}{a+b}$ |
13.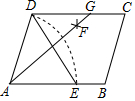 如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是( )
如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是( )
 如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是( )
如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
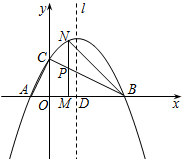 如图,已知抛物线$y=-\frac{1}{2}(x+1)(x-b)$(其中b>1)与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.
如图,已知抛物线$y=-\frac{1}{2}(x+1)(x-b)$(其中b>1)与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.