题目内容
5.在?ABCD中,AE平分∠BAD交边BC于E,DF平分∠ADC交边BC于F,若AD=11,EF=5,则AB=8或3.分析 根据平行线的性质得到∠ADF=∠DFC,由DF平分∠ADC,得到∠ADF=∠CDF,等量代换得到∠DFC=∠FDC,根据等腰三角形的判定得到CF=CD,同理BE=AB,根据平行四边形的性质得到AB=CD,AD=BC,得出AB=BE=CF=CD,分两种情况,即可得到结论.
解答  解:①如图1,在?ABCD中,∵BC=AD=11,BC∥AD,CD=AB,CD∥AB,
解:①如图1,在?ABCD中,∵BC=AD=11,BC∥AD,CD=AB,CD∥AB,
∴∠DAE=∠AEB,∠ADF=∠DFC,
∵AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,
∴∠BAE=∠DAE,∠ADF=∠CDF,
∴∠BAE=∠AEB,∠CFD=∠CDF,
∴AB=BE,CF=CD,
∴AB=BE=CF=CD
∵EF=5,
∴BC=BE+CF-EF=2AB-EF=2AB-5=11,
∴AB=8;
②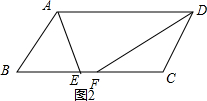 在?ABCD中,∵BC=AD=11,BC∥AD,CD=AB,CD∥AB,
在?ABCD中,∵BC=AD=11,BC∥AD,CD=AB,CD∥AB,
∴∠DAE=∠AEB,∠ADF=∠DFC,
∵AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,
∴∠BAE=∠DAE,∠ADF=∠CDF,
∴∠BAE=∠AEB,∠CFD=∠CDF,
∴AB=BE,CF=CD,
∴AB=BE=CF=CD
∵EF=5,
∴BC=BE+CF=2AB+EF=2AB+5=11,
∴AB=3;
综上所述:AB的长为8或3.
故答案为:8或3.
点评 本题考查了等腰三角形的判定和性质,平行线的性质,平行四边形的性质,解答本题的关键是判断出AB=BE=CF=CD.

练习册系列答案
相关题目
15.学生经常玩手机游戏会影响学习和生活,某校调查了20名同学某一周玩手机游戏的次数,调查结果如表所示,那么这20名同学玩手机游戏的平均数为( )
| 次数 | 2 | 4 | 5 | 8 |
| 人数 | 2 | 2 | 10 | 6 |
| A. | 5 | B. | 5.5 | C. | 6 | D. | 6.5 |
16.根据分式的基本性质,分式$\frac{-a}{a-b}$可以变形为( )
| A. | $\frac{a}{-a+b}$ | B. | $\frac{a}{a+b}$ | C. | -$\frac{-a}{a-b}$ | D. | -$\frac{a}{a+b}$ |
13.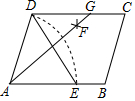 如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是( )
如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是( )
 如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是( )
如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
20.下列命题中,假命题有( )
①两点之间线段最短;②到角的两边距离相等的点在角的平分线上;
③过一点有且只有一条直线与已知直线平行;④垂直于同一直线的两条直线平行;
⑤若⊙O的弦AB,CD交于点P,则PA•PB=PC•PD.
①两点之间线段最短;②到角的两边距离相等的点在角的平分线上;
③过一点有且只有一条直线与已知直线平行;④垂直于同一直线的两条直线平行;
⑤若⊙O的弦AB,CD交于点P,则PA•PB=PC•PD.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
2.若am=2,an=4,则am+n等于( )
| A. | 5 | B. | 6 | C. | 8 | D. | 9 |
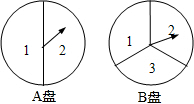 小兰和小颖用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形,转动两个转盘各一次,若两次指针所指数字之和小于4,则小兰胜,否则小颖胜(指针指在分界线时重转),这个游戏对双方公平吗?请用树状图或列表法说明理由.
小兰和小颖用下面两个可以自由转动的转盘做游戏,每个转盘被分成面积相等的几个扇形,转动两个转盘各一次,若两次指针所指数字之和小于4,则小兰胜,否则小颖胜(指针指在分界线时重转),这个游戏对双方公平吗?请用树状图或列表法说明理由.