题目内容
已知点P（1，a）与Q（b，2）关于x轴成轴对称，又有点Q（b，2）与点M（m，n）关于y轴成轴对称，则m-n的值为（ ）
| A、3 | B、-3 | C、1 | D、-1 |
考点：关于x轴、y轴对称的点的坐标
专题：
分析：根据关于x轴对称的点的坐标规律，可得b的值，根据关于y轴对称的点的坐标规律，可得m、n的值，根据有理数的减法，可得答案．
解答：解：由P（1，a）与Q（b，2）关于x轴成轴对称，得
b=1．
由点Q（b，2）与点M（m，n）关于y轴成轴对称，得
m=-b=-1，n=2．
由有理数的减法，得m-n=2-（-1）=2+1=3，
故选：A．
b=1．
由点Q（b，2）与点M（m，n）关于y轴成轴对称，得
m=-b=-1，n=2．
由有理数的减法，得m-n=2-（-1）=2+1=3，
故选：A．
点评：本题考查了关于坐标轴对称的点的坐标规律，解决本题的关键是掌握好对称点的坐标规律：（1）关于x轴对称的点，横坐标相同，纵坐标互为相反数；（2）关于y轴对称的点，纵坐标相同，横坐标互为相反数；（3）关于原点对称的点，横坐标与纵坐标都互为相反数．
练习册系列答案
相关题目
将抛物线y=3x2先向右平移1个单位，再向上平移1个单位，得到抛物线（ ）
| A、y=3（x-1）2+1 |
| B、y=3（x+1）2+1 |
| C、y=3（x-1）2-1 |
| D、y=3（x+1）2+1 |
将二次函数y=2x2向左平移3个单位，再向下平移5个单位，则得到新的图象的二次函数表达式是（ ）
| A、y=2（x-3）2-5 |
| B、y=2（x+3）2-5 |
| C、y=2（x+3）2+5 |
| D、y=2（x-3）2+5 |
二次函数y=ax2+bx+c的部分对应值如表：
下面关于二次函数及其图象说法不正确的是（ ）
| x | … | -3 | -2 | 0 | 1 | 3 | 5 | … |
| y | … | 7 | 0 | -8 | -9 | -5 | 7 | … |
| A、对称轴为x=1 |
| B、y的最大值是-9 |
| C、x=2对应的函数值y=-8 |
| D、抛物线截x轴所得的线段长是6 |
下列命题为真命题的是（ ）
| A、若直线y=-kx+2过二、四象限，则k＞0 |
| B、有两边和一角分别相等的两个三角形全等 |
| C、直线y=2x-3在y轴上的截距为3 |
| D、△ABC中，若∠A=2∠B=3∠C，那么△ABC为直角三角形 |
若y=（3+m）xm2-9是开口向下的抛物线，则m的值是（ ）
| A、m=3 | ||
| B、m=-3 | ||
C、m=
| ||
D、m=
|
已知二次函数y=a（x+m）2+m（a≠0），无论m为何实数其图象的顶点都在（ ）
| A、x轴上 | B、y轴上 |
| C、直线y=x上 | D、直线y=-x上 |
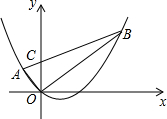如图，二次函数y=
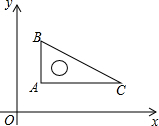如图，在平面直角坐标系中，直角三角板∠C=30°，AB=4，将直角顶点放在点（