Question

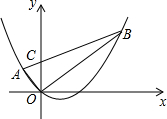如图，二次函数y=

2

3

x²-

1

3

x的图象经过△AOB的三个顶点，其中A（-1，m），B（n，n），直线AB与y轴交于点C，则△BOC的面积是（　　）

• A、

  2

  3

• B、1
• C、

  4

  3

• D、2

Answer 1

考点：二次函数图象上点的坐标特征

专题：计算题

分析：先根据二次函数图象上点的坐标特征，把A（-1，m），B（n，n）分别代入抛物线解析式可求出m和n的值，则得到A（-1，1），B（2，2），然后利用待定系数法求出直线AB的解析式，则可确定C点坐标，于是可根据三角形面积公式计算△BOC的面积

解答：解：把A（-1，m）代入y=

2

3

x²-

1

3

x得m=

2

3

+

1

3

=1，则A（-1，1），
把B（n，n）代入y=

2

3

x²-

1

3

x得

2

3

n²-

1

3

n=n，解得n₁=0（舍去），n₂=2，则B（2，2），
设直线AB的解析式为y=kx+b，
把A（-1，1），B（2，2）分别代入得

-k+b=1 2k+b=2

，解得

k= 1 3 b= 4 3

，
所以直线AB的解析式为y=

1

3

x+

4

3

，
当x=0时，y=

1

3

x+

4

3

=

4

3

，则C点坐标为（0，

4

3

），
所以△BOC的面积=

1

2

×

4

3

×2=

4

3

．
故选C．

点评：本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．也考查了三角形面积公式和待定系数法一次函数解析式．