Question

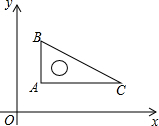如图，在平面直角坐标系中，直角三角板∠C=30°，AB=4，将直角顶点放在点（

3

，1）处，AC∥x轴，求经过点C的反比例函数的解析式．

Answer 1

考点：待定系数法求反比例函数解析式

专题：计算题

分析：先根据含30度的直角三角形三边的关系得到AC=

3

AB=4

3

，则可确定C点坐标为（5

3

，1），然后利用待定系数法求经过点C的反比例函数的解析式．

解答：解：∵∠C=30°，AB=4，
∴AC=

3

AB=4

3

，
∵AC∥x轴，
∴C点坐标为（5

3

，1），
设反比例函数解析式为y=

k

x

，
∴k=5

3

×1=-5

3

，
∴经过点C的反比例函数的解析式为y=

5 3

x

．

点评：本题考查了待定系数法求反比例函数的解析式：设出含有待定系数的反比例函数解析式y=

k

x

（k为常数，k≠0）；把已知条件（自变量与函数的对应值）代入解析式，得到待定系数的方程；解方程，求出待定系数；写出解析式．