题目内容
12.有一种螃蟹,从河里捕获后不放养最多只能活两天,如果放养在塘内,可以延长存活时间,但每天也有一定数量的蟹死去,假设放养期内蟹的个体重量基本保持不变,现有一经销商,按市场价收购了这种活蟹1000千克放养在塘内,此时市场价为每千克30元,据测算,以后每千克活蟹的市场价每天可上升1元,但是放养一天需各种费用支出400元,且平均每天还有10千克蟹死去,假定死蟹均于当天全部售出,售价都是每千克20元.(1)设X天后每千克活蟹的市场价为P元,写出P关于x的函数关系式.
(2)如果放养x天后将活蟹一次性出售,并记1000千克蟹的销售额为Q元,写出Q关于X的函数关系式.
(3)该经销商将这批蟹放养多少天后出售,可获最大利润(利润=销售总额-收购成本-费用),最大利润是多少?
分析 (1)根据市场价为每千克30元,以后每千克活蟹的市场价每天可上升1元,可列出P关于x的函数关系式;
(2)根据销售额Q=活蟹的销售额+死蟹的销售额,列出Q于x的函数关系式;
(3)根据利润=销售总额-收购成本-费用,列出利润与x天的函数关系,运用函数性质求出最值即可.
解答 解:(1)由题意知:p=30+x;
(2)由题意知:
活蟹的销售额为(1000-10x)(30+x)元,
死蟹的销售额为200x元,
∴Q=(1000-10x)(30+x)+200x=-10x2+900x+30000;
(3)设总利润为L=Q-30000-400x=-10x2+500x,
=-10(x2-50x)=-10(x2-50x+252-252)=-10(x-25)2+6250.
当x=25时,总利润最大,最大利润为6250元.
点评 此题主要考查了二次函数的应用以及二次函数最值求法,理解题意列出函数关系式是解题关键.

练习册系列答案
相关题目
17.下列事件发生的概率为0的是( )
| A. | 射击运动员只射击1次,就命中靶心 | |
| B. | 任取一个实数x,都有|x|≥0 | |
| C. | 画一个三角形,使其三边的长分别为8cm,6cm,2cm | |
| D. | 抛掷一枚质地均匀且六个面分别刻有1到6的点数的正方体骰子,朝上一面的点数为6 |
 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.以直线AB为轴,把△ABC旋转一周,求所得几何体的表面积.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.以直线AB为轴,把△ABC旋转一周,求所得几何体的表面积.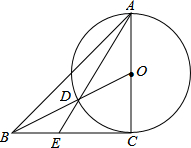 一等腰三角形ABC,AC边的中点O为圆心,以AO为半径作圆,连接BO与O交于点D,延长AD交BC于点E,已知BD=CE,求证:BC为切线.
一等腰三角形ABC,AC边的中点O为圆心,以AO为半径作圆,连接BO与O交于点D,延长AD交BC于点E,已知BD=CE,求证:BC为切线.