题目内容
11.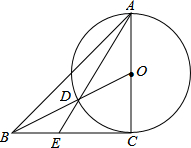 一等腰三角形ABC,AC边的中点O为圆心,以AO为半径作圆,连接BO与O交于点D,延长AD交BC于点E,已知BD=CE,求证:BC为切线.
一等腰三角形ABC,AC边的中点O为圆心,以AO为半径作圆,连接BO与O交于点D,延长AD交BC于点E,已知BD=CE,求证:BC为切线.
分析 延长BO交⊙O于F,连接CF、DC,先证得DE∥CF,得出$\frac{BD}{DF}$=$\frac{BE}{EC}$,继而得出$\frac{BD}{BC}$=$\frac{BE}{BD}$,从而证得△BDE∽△BCD,得出∠BDE=∠CAD,即可证得∠ACB=90°.
解答 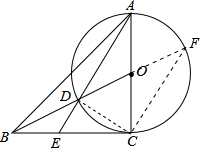 证明:延长BO交⊙O于F,连接CF、DC,
证明:延长BO交⊙O于F,连接CF、DC,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠BDE=∠OAD,
∵∠F=∠OAD,
∴∠F=∠BDE,
∴DE∥CF,
∴$\frac{BD}{DF}$=$\frac{BE}{EC}$,
∵BD=EC,AC=DF,BC=AC,
∴$\frac{BD}{BC}$=$\frac{BE}{BD}$,
∵∠DBE=∠CBD,
∴△BDE∽△BCD,
∴∠BCD=∠BDE,
∵∠BDE=∠CAD,
∴∠BCD=∠CAD,
∵AC是直径,
∴∠ADC=90°,
∴∠CAD+∠ACD=90°,
∴∠BCD+∠ACD=90°,
即∠ACB=90°,
∴BC为切线.
点评 本题考查了切线的判定,圆周角定理,平行线的判定和性质,三角形相似的判定和性质等,作出辅助线构建DE∥CF是解题的关键.

练习册系列答案
相关题目
11.不等式2x+5>4的解集是( )
| A. | x>-2 | B. | x<-2 | C. | x>-$\frac{1}{2}$ | D. | x<-$\frac{1}{2}$ |
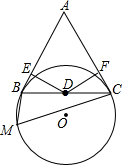 如图,已知BC是⊙O的弦,A是⊙O外一点,△ABC为正三角形,D为BC的中点,M为⊙O上一点,并且∠BMC=60°.
如图,已知BC是⊙O的弦,A是⊙O外一点,△ABC为正三角形,D为BC的中点,M为⊙O上一点,并且∠BMC=60°.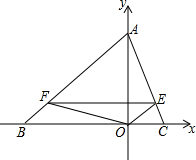 如图,等腰△ABC中,BA=BC,AO=3CO=6.动点F在BA上以每分钟5个单位长度的速度从B点出发向A点移动,过F作FE∥BC交AC边于E点,连结FO、EO.
如图,等腰△ABC中,BA=BC,AO=3CO=6.动点F在BA上以每分钟5个单位长度的速度从B点出发向A点移动,过F作FE∥BC交AC边于E点,连结FO、EO. 如图,在△ABC中,BE平分∠ABC,CE平分∠ACD,BE,CE相交于点E.求证:∠E=$\frac{1}{2}$∠A.
如图,在△ABC中,BE平分∠ABC,CE平分∠ACD,BE,CE相交于点E.求证:∠E=$\frac{1}{2}$∠A.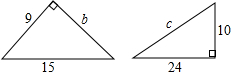 求图中直角三角形中未知的长度:b=12,c=26.
求图中直角三角形中未知的长度:b=12,c=26.