题目内容
20.(1)x2+4x+2=0(2)x2-6x+9=(5-2x)2.
分析 (1)本题二次项系数为1,一次项系数为4,适合于用配方法.
(2)把方程左边化成一个完全平方式,那么将出现两个完全平方式相等,则这两个式子相等或互为相反数,据此即可转化为两个一元一次方程即可求解.
解答 解:(1)x2+4x+22=-2+22,
即(x+2)2=2$\sqrt{2}$,
x1=-2+$\sqrt{2}$,x2=-2-$\sqrt{2}$;
(2)(x-3)2=(5-2x)2,
即(x-3+5-2x)(x-3-5+2x)=0,
x1=2,x2=$\frac{8}{3}$.
点评 (1)本题考查了配方法解一元二次方程,选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.
(2)本题考查了因式分解法解一元二次方程,解一元二次方程的基本思想是降次,把一元二次方程转化为一元一次方程,从而求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.不等式2x+5>4的解集是( )
| A. | x>-2 | B. | x<-2 | C. | x>-$\frac{1}{2}$ | D. | x<-$\frac{1}{2}$ |
8.$\sqrt{64}$的立方根等于( )
| A. | 4 | B. | -4 | C. | ±4 | D. | 2 |
5.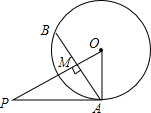 如图,PA切⊙O于点A,弦AB⊥OP,垂足为M,AB=4,OM=1,则PA的长为( )
如图,PA切⊙O于点A,弦AB⊥OP,垂足为M,AB=4,OM=1,则PA的长为( )
 如图,PA切⊙O于点A,弦AB⊥OP,垂足为M,AB=4,OM=1,则PA的长为( )
如图,PA切⊙O于点A,弦AB⊥OP,垂足为M,AB=4,OM=1,则PA的长为( )| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 4$\sqrt{5}$ |
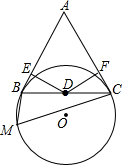 如图,已知BC是⊙O的弦,A是⊙O外一点,△ABC为正三角形,D为BC的中点,M为⊙O上一点,并且∠BMC=60°.
如图,已知BC是⊙O的弦,A是⊙O外一点,△ABC为正三角形,D为BC的中点,M为⊙O上一点,并且∠BMC=60°.