题目内容
13. 禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处距离为200海里,可疑船只正沿南偏东45°方向航行,我渔政船迅速沿北偏东30°方向前去拦截,经历4小时刚好在C处将可疑船只拦截.求该可疑船只航行的平均速度(结果保留根号).
禁渔期间,我渔政船在A处发现正北方向B处有一艘可疑船只,测得A、B两处距离为200海里,可疑船只正沿南偏东45°方向航行,我渔政船迅速沿北偏东30°方向前去拦截,经历4小时刚好在C处将可疑船只拦截.求该可疑船只航行的平均速度(结果保留根号).
分析 先过点C作CD⊥AB,垂足为点D,设BD=x海里,得出AD=(200-x)海里,在Rt△BCD中,根据tan45°=$\frac{CD}{BD}$,求出CD,再根据BD=CD求出BD,在Rt△BCD中,根据cos45°=$\frac{BD}{BC}$,求出BC,从而得出答案.
解答 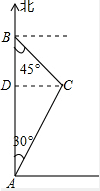 解:过点C作CD⊥AB,垂足为点D,设BD=x海里,则AD=(200-x)海里,
解:过点C作CD⊥AB,垂足为点D,设BD=x海里,则AD=(200-x)海里,
∵∠ABC=45°,
∴BD=CD=x,
∵∠BAC=30°,
∴tan30°=$\frac{CD}{AD}$,
在Rt△ACD中,则CD=AD•tan30°=$\frac{\sqrt{3}}{3}$(200-x),
则x=$\frac{\sqrt{3}}{3}$(200-x),
解得,x=100$\sqrt{3}$-100,
即BD=100$\sqrt{3}$-100,
在Rt△BCD中,cos45°=$\frac{BD}{BC}$,
解得:BC=100$\sqrt{6}$-100$\sqrt{2}$,
则(100$\sqrt{6}$-100$\sqrt{2}$)÷4=25($\sqrt{6}$-$\sqrt{2}$)(海里/时),
则该可疑船只的航行速度约为25($\sqrt{6}$-$\sqrt{2}$)海里/时.
点评 此题考查了解直角三角形的应用,用到的知识点是方向角含义、三角函数的定义,关键是根据题意画出图形,构造直角三角形.

练习册系列答案
相关题目
5.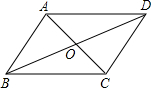 如图,?ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )
如图,?ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )
 如图,?ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )
如图,?ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )| A. | 13 | B. | 17 | C. | 20 | D. | 26 |
8.2016年“五一”假期期间,某市接待旅游总人数达到了9 180 000人次,将9 180 000用科学记数法表示应为( )
| A. | 918×104 | B. | 9.18×105 | C. | 9.18×106 | D. | 9.18×107 |
18.化简$\frac{{x}^{2}-{y}^{2}}{(y-x)^{2}}$的结果是( )
| A. | -1 | B. | 1 | C. | $\frac{x+y}{y-x}$ | D. | $\frac{x+y}{x-y}$ |
5.-$\sqrt{5}$的绝对值是( )
| A. | -$\frac{1}{\sqrt{5}}$ | B. | -$\sqrt{5}$ | C. | $\sqrt{5}$ | D. | 5 |
 如图,已知BD是矩形ABCD的对角线.
如图,已知BD是矩形ABCD的对角线.
 C. ―
C. ―