题目内容
20.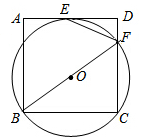 如图,过正方形ABCD顶点B,C的⊙O与AD相切于点E,与CD相交于点F,连接EF.
如图,过正方形ABCD顶点B,C的⊙O与AD相切于点E,与CD相交于点F,连接EF.(1)求证:EF平分∠BFD.
(2)若tan∠FBC=$\frac{3}{4}$,DF=$\sqrt{5}$,求EF的长.
分析 (1)根据切线的性质得到OE⊥AD,由四边形ABCD的正方形,得到CD⊥AD,推出OE∥CD,根据平行线的性质得到∠EFD=∠OEF,由等腰三角形的性质得到∠OEF=∠OFE,根据角平分线的定义即可得到结论;
(2)连接PF,由BF是⊙O的直径,得到∠BPF=90°,推出四边形BCFP是矩形,根据tan∠FBC=$\frac{3}{4}$,设CF=3x,BC=4x,于是得到3x+$\sqrt{5}$=4x,x=$\sqrt{5}$,求得AD=BC=4$\sqrt{5}$,推出DF∥OE∥AB于是得到DE:AE=OF:OB=1:1即可得到结论.
解答 解:(1)连接OE,BF,PF,
∵∠C=90°,
∴BF是⊙O的直径,
∵⊙O与AD相切于点E,
∴OE⊥AD,
∵四边形ABCD的正方形,
∴CD⊥AD,
∴OE∥CD,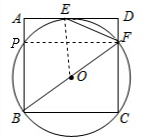
∴∠EFD=∠OEF,
∵OE=OF,
∴∠OEF=∠OFE,
∴∠OFE=∠EFD,
∴EF平分∠BFD;
(2)连接PF,
∵BF是⊙O的直径,
∴∠BPF=90°,
∴四边形BCFP是矩形,
∴PF=BC,
∵tan∠FBC=$\frac{3}{4}$,
设CF=3x,BC=4x,
∴3x+$\sqrt{5}$=4x,x=$\sqrt{5}$,
∴AD=BC=4$\sqrt{5}$,
∵点E是切点,
∴OE⊥AD
∴DF∥OE∥AB
∴DE:AE=OF:OB=1:1
∴DE=$\frac{1}{2}$AD=2$\sqrt{5}$,
∴EF=$\sqrt{D{E}^{2}+D{F}^{2}}$=5.
点评 本题考查了切线的性质,正方形的性质,圆周角定理,等腰三角形的性质,平行线的性质,切割线定理,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
13.菱形ABCD中,对角线AC、BD相交于O,H为AD边中点,OH的长等于3,则菱形ABCD的周长为( )
| A. | 24 | B. | 12 | C. | 9 | D. | 18 |
9.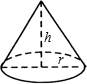 如图,圆锥的底面半径r为6cm,高h为8cm,则圆锥的侧面积为( )
如图,圆锥的底面半径r为6cm,高h为8cm,则圆锥的侧面积为( )
 如图,圆锥的底面半径r为6cm,高h为8cm,则圆锥的侧面积为( )
如图,圆锥的底面半径r为6cm,高h为8cm,则圆锥的侧面积为( )| A. | 30πcm2 | B. | 48πcm2 | C. | 60πcm2 | D. | 80πcm2 |
5.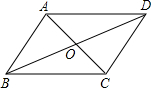 如图,?ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )
如图,?ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )
 如图,?ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )
如图,?ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )| A. | 13 | B. | 17 | C. | 20 | D. | 26 |
9.下列各数中最小的是( )
| A. | 0 | B. | -3 | C. | -$\sqrt{3}$ | D. | 1 |
8.2016年“五一”假期期间,某市接待旅游总人数达到了9 180 000人次,将9 180 000用科学记数法表示应为( )
| A. | 918×104 | B. | 9.18×105 | C. | 9.18×106 | D. | 9.18×107 |

 如图为A、B、C三点在坐标平面上的位置图.若A、B、C的x坐标的数字总和为a,y坐标的数字总和为b,则a-b之值为何?( )
如图为A、B、C三点在坐标平面上的位置图.若A、B、C的x坐标的数字总和为a,y坐标的数字总和为b,则a-b之值为何?( )