题目内容
17. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,-4),连接AO,AO=5,sin∠AOC=$\frac{3}{5}$.
如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,-4),连接AO,AO=5,sin∠AOC=$\frac{3}{5}$.(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积.
分析 (1)过点A作AE⊥x轴于点E,设反比例函数解析式为y=$\frac{k}{x}$.通过解直角三角形求出线段AE、OE的长度,即求出点A的坐标,再由点A的坐标利用待定系数法求出反比例函数解析式即可;
(2)由点B在反比例函数图象上可求出点B的坐标,设直线AB的解析式为y=ax+b,由点A、B的坐标利用待定系数法求出直线AB的解析式,令该解析式中y=0即可求出点C的坐标,再利用三角形的面积公式即可得出结论.
解答 解:(1)过点A作AE⊥x轴于点E,如图所示.
设反比例函数解析式为y=$\frac{k}{x}$.
∵AE⊥x轴,
∴∠AEO=90°.
在Rt△AEO中,AO=5,sin∠AOC=$\frac{3}{5}$,∠AEO=90°,
∴AE=AO•sin∠AOC=3,OE=$\sqrt{A{O}^{2}-A{E}^{2}}$=4,
∴点A的坐标为(-4,3).
∵点A(-4,3)在反比例函数y=$\frac{k}{x}$的图象上,
∴3=$\frac{k}{-4}$,解得:k=-12.
∴反比例函数解析式为y=-$\frac{12}{x}$.
(2)∵点B(m,-4)在反比例函数y=-$\frac{12}{x}$的图象上,
∴-4=-$\frac{12}{m}$,解得:m=3,
∴点B的坐标为(3,-4).
设直线AB的解析式为y=ax+b,
将点A(-4,3)、点B(3,-4)代入y=ax+b中得:
$\left\{\begin{array}{l}{3=-4a+b}\\{-4=3a+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-1}\\{b=-1}\end{array}\right.$,
∴一次函数解析式为y=-x-1.
令一次函数y=-x-1中y=0,则0=-x-1,
解得:x=-1,即点C的坐标为(-1,0).
S△AOB=$\frac{1}{2}$OC•(yA-yB)=$\frac{1}{2}$×1×[3-(-4)]=$\frac{7}{2}$.
点评 本题考查了反比例函数与一次函数的交点问题、待定系数法求函数解析式以及三角形的面积公式,解题的关键是:(1)求出点A的坐标;(2)求出直线AB的解析式.本题属于基础题,难度不大,解决该题型题目时,根据点的坐标利用待定系数法求出函数解析式是关键.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案| A. | x≤1 | B. | x≥1 | C. | x≥-2 | D. | -2≤x<4 |
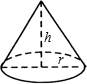 如图,圆锥的底面半径r为6cm,高h为8cm,则圆锥的侧面积为( )
如图,圆锥的底面半径r为6cm,高h为8cm,则圆锥的侧面积为( )| A. | 30πcm2 | B. | 48πcm2 | C. | 60πcm2 | D. | 80πcm2 |
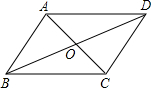 如图,?ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )
如图,?ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为( )| A. | 13 | B. | 17 | C. | 20 | D. | 26 |
| A. | 0 | B. | -3 | C. | -$\sqrt{3}$ | D. | 1 |
| A. | -$\frac{1}{\sqrt{5}}$ | B. | -$\sqrt{5}$ | C. | $\sqrt{5}$ | D. | 5 |
 如图为A、B、C三点在坐标平面上的位置图.若A、B、C的x坐标的数字总和为a,y坐标的数字总和为b,则a-b之值为何?( )
如图为A、B、C三点在坐标平面上的位置图.若A、B、C的x坐标的数字总和为a,y坐标的数字总和为b,则a-b之值为何?( )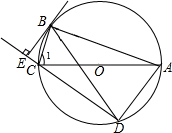 如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,BE⊥DC交DC的延长线于点E.
如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,BE⊥DC交DC的延长线于点E. 如图,已知BD是矩形ABCD的对角线.
如图,已知BD是矩形ABCD的对角线.