题目内容
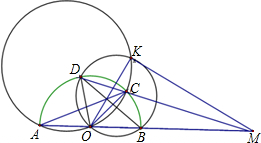 在半圆O中,AB为直径,一直线交半圆周于C、D,交AB延长线于M(MB<MA,AC<MD),设K是△AOC与△DOB的外接圆除点O外的另一个交点,求证:∠MKO=90°.
在半圆O中,AB为直径,一直线交半圆周于C、D,交AB延长线于M(MB<MA,AC<MD),设K是△AOC与△DOB的外接圆除点O外的另一个交点,求证:∠MKO=90°.考点:四点共圆
专题:证明题
分析:连接CK,BK,BC,由AB是⊙O直径可得∠OAC+∠ABC=90°,根据圆周角定理可得∠OAC=∠OKC,要证∠MKO=90°,只需证到∠ABC=∠MKC,只需证到B、C、K、M四点共圆,只需证到∠BMC=∠BKC即可.
解答:证明:连接CK,BK,BC,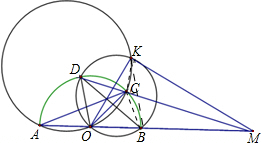 如图所示.
如图所示.
∵AB是⊙O直径,
∴∠ACB=90°,
∴∠OAC+∠ABC=90°.
∵A、B、C、D四点共圆,
∴∠BDC=∠BAC.
∵A、O、C、K四点共圆,
∴∠CKO=∠OAC.
∵D、O、B、K四点共圆,
∴∠BKO=∠BDO.
∴∠BKC=∠BKO-∠CKO=∠BDO-∠OAC.
∵OB=OD,
∴∠ABD=∠BDO.
∴∠BMC=∠ABD-∠BDC=∠BDO-∠BAC=∠BKC.
∴B、C、K、M四点共圆.
∴∠ABC=∠MKC.
∴∠MKO=∠MKC+∠CKO=∠ABC+∠OAC=90°.
 如图所示.
如图所示.∵AB是⊙O直径,
∴∠ACB=90°,
∴∠OAC+∠ABC=90°.
∵A、B、C、D四点共圆,
∴∠BDC=∠BAC.
∵A、O、C、K四点共圆,
∴∠CKO=∠OAC.
∵D、O、B、K四点共圆,
∴∠BKO=∠BDO.
∴∠BKC=∠BKO-∠CKO=∠BDO-∠OAC.
∵OB=OD,
∴∠ABD=∠BDO.
∴∠BMC=∠ABD-∠BDC=∠BDO-∠BAC=∠BKC.
∴B、C、K、M四点共圆.
∴∠ABC=∠MKC.
∴∠MKO=∠MKC+∠CKO=∠ABC+∠OAC=90°.
点评:本题考查了四点共圆的判定、圆周角定理、圆内接四边形的性质等知识,而证到B、C、K、M四点共圆是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图.已知0是直线AB上一点,∠1=50°,0D平分∠BOC,则∠2的度数是( )
如图.已知0是直线AB上一点,∠1=50°,0D平分∠BOC,则∠2的度数是( )| A、25° | B、50° |
| C、65° | D、70° |
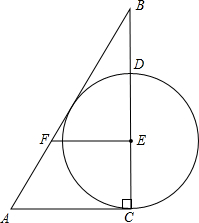 已知:如图,Rt△ABC,∠ACB=90°,点E是边BC上一点,过点E作FE⊥BC(垂足为E)交AB于点F,且EF=AF,以点E为圆心,EC长为半径作⊙E交BC于点D
已知:如图,Rt△ABC,∠ACB=90°,点E是边BC上一点,过点E作FE⊥BC(垂足为E)交AB于点F,且EF=AF,以点E为圆心,EC长为半径作⊙E交BC于点D 在?ABCD中,点E在BC边上,点F在BC边的延长线上,且BE=CF.
在?ABCD中,点E在BC边上,点F在BC边的延长线上,且BE=CF.