题目内容
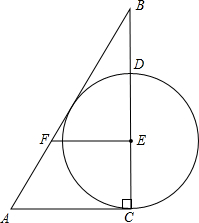 已知:如图,Rt△ABC,∠ACB=90°,点E是边BC上一点,过点E作FE⊥BC(垂足为E)交AB于点F,且EF=AF,以点E为圆心,EC长为半径作⊙E交BC于点D
已知:如图,Rt△ABC,∠ACB=90°,点E是边BC上一点,过点E作FE⊥BC(垂足为E)交AB于点F,且EF=AF,以点E为圆心,EC长为半径作⊙E交BC于点D(1)求证:斜边AB是⊙E的切线;
(2)设AB与⊙E相切的切点为G,AC=8,EF=5,连DA、DG,求AE的长.
考点:切线的判定
专题:
分析:(1)过E作EG⊥AB于G,过F作FM⊥AC于M,推出四边形FMCE是矩形,求出CE=FM,EF=CM,求出∠GFE=∠A,证△EGF≌△FMA,推出FM=EG=CE,根据切线的判定推出即可;
(2)求出FG,根据勾股定理求出半径,再根据勾股定理求出AE即可.
(2)求出FG,根据勾股定理求出半径,再根据勾股定理求出AE即可.
解答:(1)证明:
过E作EG⊥AB于G,过F作FM⊥AC于M,
则∠EGF=∠FMA=90°,
∵∠ACB=90°,
∴FM∥BC,
∵EF∥AC,
∴四边形FMCE是矩形,
∴CE=FM,EF=CM,
∵EF∥AC,
∴∠GFE=∠A,
在△EGF和△FMA中
∴△EGF≌△FMA(AAS),
∴FM=EG,
∵FM=CE,
∴EG=CE,
∵EG⊥AB,
∴斜边AB是⊙E的切线;
(2)解:
∵∠ACB=90°,
∴AC是⊙E的切线,
∵AB是⊙E的切线,AC=8,
∴AG=AC=8,
∵AF=EF=5,
∴FG=8-5=3,
在Rt△EGF中,由勾股定理得:EG=
=4,
即CE=4,
在Rt△ACE中,AC=8,CE=4,由勾股定理得:AE=
=4
.

过E作EG⊥AB于G,过F作FM⊥AC于M,
则∠EGF=∠FMA=90°,
∵∠ACB=90°,
∴FM∥BC,
∵EF∥AC,
∴四边形FMCE是矩形,
∴CE=FM,EF=CM,
∵EF∥AC,
∴∠GFE=∠A,
在△EGF和△FMA中
|
∴△EGF≌△FMA(AAS),
∴FM=EG,
∵FM=CE,
∴EG=CE,
∵EG⊥AB,
∴斜边AB是⊙E的切线;
(2)解:

∵∠ACB=90°,
∴AC是⊙E的切线,
∵AB是⊙E的切线,AC=8,
∴AG=AC=8,
∵AF=EF=5,
∴FG=8-5=3,
在Rt△EGF中,由勾股定理得:EG=
| 55-32 |
即CE=4,
在Rt△ACE中,AC=8,CE=4,由勾股定理得:AE=
| 42+82 |
| 5 |
点评:本题考查了矩形的性质和判定,全等三角形的性质和判定,切线的性质和判定,勾股定理的应用,题目比较好,综合性比较强,有一定的难度.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
把三角形三边的长度都扩大为原来的2倍,则锐角A的正弦函数值( )
| A、扩大为原来的2倍 | ||
B、缩小为原来的
| ||
| C、不变 | ||
| D、不能确定 |
 如图,正方形ABCD中,M为BD上一点,N为BC上一点,AM=MN,NP⊥BD于P.
如图,正方形ABCD中,M为BD上一点,N为BC上一点,AM=MN,NP⊥BD于P. 如图,△ABC中,∠ACB=90°,AC>BC,CD、CE分别为斜边AB上的高和中线,若tan∠DCE=
如图,△ABC中,∠ACB=90°,AC>BC,CD、CE分别为斜边AB上的高和中线,若tan∠DCE=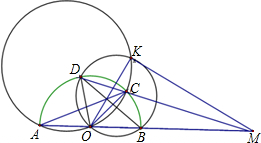 在半圆O中,AB为直径,一直线交半圆周于C、D,交AB延长线于M(MB<MA,AC<MD),设K是△AOC与△DOB的外接圆除点O外的另一个交点,求证:∠MKO=90°.
在半圆O中,AB为直径,一直线交半圆周于C、D,交AB延长线于M(MB<MA,AC<MD),设K是△AOC与△DOB的外接圆除点O外的另一个交点,求证:∠MKO=90°.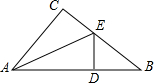 在△ABC中,∠C=90°,AC=6,BC=8,AE平分∠CAE,ED⊥AB,求BE的长.
在△ABC中,∠C=90°,AC=6,BC=8,AE平分∠CAE,ED⊥AB,求BE的长.