题目内容
 在?ABCD中,点E在BC边上,点F在BC边的延长线上,且BE=CF.
在?ABCD中,点E在BC边上,点F在BC边的延长线上,且BE=CF.(1)求证:四边形AEFD是平行四边形;
(2)连接AF,分别交DE、CD于M、N,若∠B=∠AME,求证:ND•AD=AN•ME.
考点:平行四边形的判定与性质,相似三角形的判定与性质
专题:证明题
分析:(1)由于ABCD是平行四边形,得出AD∥BC,AD=BC,根据已知得出EF=BC=AD,根据对边平行且相等的四边形是平行四边形即可证得;
(2)先证得∠ADC=∠DMN,进而得出△ADN∽△DMN,根据相似三角形对应边成比例得出ND•AD=AN•MD,因为DM=ME,即可证得结论.
(2)先证得∠ADC=∠DMN,进而得出△ADN∽△DMN,根据相似三角形对应边成比例得出ND•AD=AN•MD,因为DM=ME,即可证得结论.
解答:证明:(1)∵ABCD是平行四边形,
∴AD∥BC,AD=BC,
又∵BE=CF,
∴EF=BC=AD,
∴四边形AEFD是平行四边形.
(2)∵ABCD是平行四边形,
∴∠B=∠ADC,
∵∠B=∠AME=∠DMN,
∴∠ADC=∠DMN,
∴△ADN∽△DMN,
∴
=
,
∴ND•AD=AN•MD,
∵DM=ME
∴ND•AD=AN•ME.
∴AD∥BC,AD=BC,
又∵BE=CF,
∴EF=BC=AD,
∴四边形AEFD是平行四边形.
(2)∵ABCD是平行四边形,
∴∠B=∠ADC,
∵∠B=∠AME=∠DMN,
∴∠ADC=∠DMN,
∴△ADN∽△DMN,
∴
| AN |
| AD |
| DN |
| DM |
∴ND•AD=AN•MD,
∵DM=ME
∴ND•AD=AN•ME.
点评:本题考查了平行四边形的性质以及判定,相似三角形的判定和性质,熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目
已知三角形三边为a、b、c,其中a、b两边满足
+
=0,那么这个三角形的最大边c的取值范围是( )
| a2-12a+36 |
| b-8 |
| A、c>8 |
| B、8<c<14 |
| C、6<c<8 |
| D、2<c<14 |
在Rt△ABC中,∠C=90°,AC=3,AB=4,那么cosA的值是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
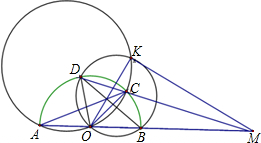 在半圆O中,AB为直径,一直线交半圆周于C、D,交AB延长线于M(MB<MA,AC<MD),设K是△AOC与△DOB的外接圆除点O外的另一个交点,求证:∠MKO=90°.
在半圆O中,AB为直径,一直线交半圆周于C、D,交AB延长线于M(MB<MA,AC<MD),设K是△AOC与△DOB的外接圆除点O外的另一个交点,求证:∠MKO=90°.
 如图,在△ABC中,EG∥BC,BF平分∠ABC,CF平分∠ACB,AB=10,AC=12,△AEG的周长为
如图,在△ABC中,EG∥BC,BF平分∠ABC,CF平分∠ACB,AB=10,AC=12,△AEG的周长为