题目内容
 如图,AB是⊙O的直径,P是AB上一点,C,D分别是圆上的点,且∠CPB=∠DPB,
如图,AB是⊙O的直径,P是AB上一点,C,D分别是圆上的点,且∠CPB=∠DPB, |
| BD |
 |
| BC |
考点:圆心角、弧、弦的关系,全等三角形的判定与性质
专题:
分析:连接OC、OD、BC、BD,根据同圆中相等的弧所对的圆心角相等以及等腰三角形的性质证得∠CBO=∠DBO,即可根据SAS证得△BCO≌△BDO,则PC=PD可以证得.
解答: 答:PC=PD.
答:PC=PD.
证明:连接OC、OD、BC、BD.
∵
=
,
∴BC=BD,∠BOC=∠BOD,
又∵OC=OB,OB=OD,
∴∠CBO=∠DBO,
在△BCO和△BDO中,
,
∴△BCO≌△BDO(SAS),
∴PC=PD.
 答:PC=PD.
答:PC=PD.证明:连接OC、OD、BC、BD.
∵
 |
| BD |
 |
| BC |
∴BC=BD,∠BOC=∠BOD,
又∵OC=OB,OB=OD,
∴∠CBO=∠DBO,
在△BCO和△BDO中,
|
∴△BCO≌△BDO(SAS),
∴PC=PD.
点评:本题考查了弧、弦、圆心角之间的关系以及三角形全等的判定与性质,证明∠CBO=∠DBO是关键.

练习册系列答案
相关题目
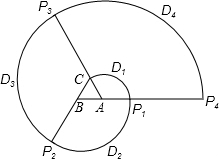 如图,正△ABC的边长为1 cm,将线段AC绕点A顺时针旋转120°至AP1,形成扇形D1;将线段BP1 绕点B顺时针旋转120°至BP2,形成扇形D2;将线段CP2 绕点C顺时针旋转120°至CP3,形成扇形D3;将线段AP3 绕点A顺时针旋转120°至AP4,形成扇形D4 …设ln为扇形Dn的弧长(n=1,2,3,…),回答下列问题:
如图,正△ABC的边长为1 cm,将线段AC绕点A顺时针旋转120°至AP1,形成扇形D1;将线段BP1 绕点B顺时针旋转120°至BP2,形成扇形D2;将线段CP2 绕点C顺时针旋转120°至CP3,形成扇形D3;将线段AP3 绕点A顺时针旋转120°至AP4,形成扇形D4 …设ln为扇形Dn的弧长(n=1,2,3,…),回答下列问题: