题目内容
计算:
(1)(-
)0+(-3)3-(-0.2)2011×(5)2011;
(2)2(m+1)2-(2m+1)(2m-1)
(3)
,并将解集在数轴上表示出来.
(1)(-
| 1 |
| 2 |
(2)2(m+1)2-(2m+1)(2m-1)
(3)
|
考点:解一元一次不等式组,整式的混合运算,零指数幂,在数轴上表示不等式的解集
专题:计算题
分析:(1)首先计算乘方,逆用积的乘方公式,然后计算加减即可;
(2)首先利用完全平方公式和平方差公式计算,然后去括号、合并同类项即可求解;
(3)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.
(2)首先利用完全平方公式和平方差公式计算,然后去括号、合并同类项即可求解;
(3)首先解每个不等式,两个不等式的解集的公共部分就是不等式组的解集.
解答:解:(1)原式=1-27-(-0.2×5)2011
=1-27+1
=-25;
(2)原式=2(m2+2m+1)-(4m2-1)
=2m2+2m+2-4m2+1
=-2m2+2m+3;
(3)
,
解①得:x<-
,
解②得:x≥-1.
则不等式组的解集是:-1≤x<-
.

=1-27+1
=-25;
(2)原式=2(m2+2m+1)-(4m2-1)
=2m2+2m+2-4m2+1
=-2m2+2m+3;
(3)
|
解①得:x<-
| 1 |
| 2 |
解②得:x≥-1.
则不等式组的解集是:-1≤x<-
| 1 |
| 2 |

点评:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

练习册系列答案
相关题目
 如图,AB是⊙O的直径,P是AB上一点,C,D分别是圆上的点,且∠CPB=∠DPB,
如图,AB是⊙O的直径,P是AB上一点,C,D分别是圆上的点,且∠CPB=∠DPB,
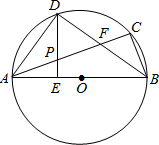 已知:如图,△ABC内接于⊙O,AB为直径.∠CBA的平分线交AC于点F,交⊙O于点D.DE⊥AB于点E,且交AC于点P.连结AD,
已知:如图,△ABC内接于⊙O,AB为直径.∠CBA的平分线交AC于点F,交⊙O于点D.DE⊥AB于点E,且交AC于点P.连结AD,