题目内容
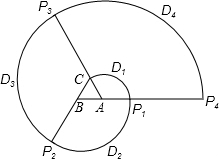 如图,正△ABC的边长为1 cm,将线段AC绕点A顺时针旋转120°至AP1,形成扇形D1;将线段BP1 绕点B顺时针旋转120°至BP2,形成扇形D2;将线段CP2 绕点C顺时针旋转120°至CP3,形成扇形D3;将线段AP3 绕点A顺时针旋转120°至AP4,形成扇形D4 …设ln为扇形Dn的弧长(n=1,2,3,…),回答下列问题:
如图,正△ABC的边长为1 cm,将线段AC绕点A顺时针旋转120°至AP1,形成扇形D1;将线段BP1 绕点B顺时针旋转120°至BP2,形成扇形D2;将线段CP2 绕点C顺时针旋转120°至CP3,形成扇形D3;将线段AP3 绕点A顺时针旋转120°至AP4,形成扇形D4 …设ln为扇形Dn的弧长(n=1,2,3,…),回答下列问题:(1)按要求填表;
| n | 1 | 2 | 3 | 4 |
| ln |
(3)圆锥的侧面积实际上是展开图的
考点:圆锥的计算,弧长的计算,扇形面积的计算
专题:规律型
分析:(1)(2)从上图中可以找出规律,弧长的圆心角不变都是120度,变化的是半径,而且第一次是1,第二次是2,第三次是3,依此下去,然后按照弧长公式计算.
(3)利用圆锥的两种面积的计算方法直接回答即可.
(3)利用圆锥的两种面积的计算方法直接回答即可.
解答:解:(1)根据弧长公式得l1=
=
;
l2=
=
;
l3=
=2π;
l4=
=
(2)根据上述规律可知:
1n=
=2π×6400000,
解得n=1.92×107.
(3)圆锥的侧面积实际上是展开图的面积.若设圆锥侧面展开图的圆心角为n°,则它的侧面积是
;若已知圆锥的母线长l和圆锥的底面半径r,则它的侧面积是πrl.
故答案为:面积,
,πrl
| 120π×1 |
| 180 |
| 2π |
| 3 |
l2=
| 120π×2 |
| 180 |
| 4π |
| 3 |
l3=
| 120π×3 |
| 180 |
l4=
| 120π×4 |
| 180 |
| 8π |
| 3 |
| n | 1 | 2 | 3 | 4 | ||||||
| ln |
|
|
2π |
|
1n=
| 120π×n |
| 180 |
解得n=1.92×107.
(3)圆锥的侧面积实际上是展开图的面积.若设圆锥侧面展开图的圆心角为n°,则它的侧面积是
| nπr2 |
| 360 |
故答案为:面积,
| nπr2 |
| 360 |
点评:本题考查了扇形面积的计算和弧长的计算.熟记公式是解题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
 如图,AB是⊙O的直径,P是AB上一点,C,D分别是圆上的点,且∠CPB=∠DPB,
如图,AB是⊙O的直径,P是AB上一点,C,D分别是圆上的点,且∠CPB=∠DPB,
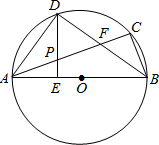 已知:如图,△ABC内接于⊙O,AB为直径.∠CBA的平分线交AC于点F,交⊙O于点D.DE⊥AB于点E,且交AC于点P.连结AD,
已知:如图,△ABC内接于⊙O,AB为直径.∠CBA的平分线交AC于点F,交⊙O于点D.DE⊥AB于点E,且交AC于点P.连结AD, 如图,已知AB⊥CD垂足为O,EF经过点O.如果∠1=40°,则∠2=
如图,已知AB⊥CD垂足为O,EF经过点O.如果∠1=40°,则∠2=