题目内容
1.已知a、b分别是等腰三角形的一腰和底边的长,求证:关于x的二次三项式x2-4ax+b2一定能在实数范围内分解因式.分析 根据三角形三边的关系,可得2a+b>0,2a-b>0,根据根的判别式,可得方程有两个不相等的实数根,可得答案.
解答 证明:∵a、b分别是等腰三角形的一腰和底边的长,
∴2a+b>0,2a>b,
.∴2a-b>0.
对于方程x2-4ax+b2=0,
∵△=16a2-4b2=(4a+2b)(4a-2b)=4(2a+b)(2a-b)
∴△=4(2a+b)(2a-b)>0,
∴方程x2-4ax+b2=0有两个不相等的实数根,
∴关于x的二次三项式x2-4ax+b2一定能在实数范围内分解因式.
点评 本题考查了实数范围内分解因式,利用根的判别式得出方程有两个不相等的实数根是解题关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
12.下列各组数中,全是勾股数的一组是( )
| A. | 2,3,4;6,8,10;5,12,13 | B. | 3,4,5;10,24,26;7,24,25 | ||
| C. | $\frac{1}{4}$,$\frac{1}{4}$,$\frac{1}{5}$;8,15,17;30,40,50 | D. | 0.4,1.2,1.3;6,8,10;9,40,41 |
9.如果用符号“[a]”表示数字a的整数部分,例如[5.7]=5,[$\frac{5}{3}$]=1,[$\frac{1}{\frac{1}{2001}+\frac{1}{2002}+\frac{1}{2003}…+\frac{1}{2039}}$]=( )
| A. | 52 | B. | 100 | C. | 150 | D. | 200 |
16.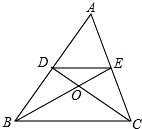 如图已知:△ABC中,DE∥BC,BE,CD交于点O,S△DOE:S△BOC=4:25,则AD:DB=( )
如图已知:△ABC中,DE∥BC,BE,CD交于点O,S△DOE:S△BOC=4:25,则AD:DB=( )
 如图已知:△ABC中,DE∥BC,BE,CD交于点O,S△DOE:S△BOC=4:25,则AD:DB=( )
如图已知:△ABC中,DE∥BC,BE,CD交于点O,S△DOE:S△BOC=4:25,则AD:DB=( )| A. | 2:5 | B. | 2:3 | C. | 4:9 | D. | 3:5 |
10.沪蓉高速大别山特长隧道贯通,全长4901m,将4901用科学记数法表示为( )
| A. | 49.01×102 | B. | 4.901×103 | C. | 490.1×10 | D. | 0.4901×104 |
17.已知某种细菌的直径为0.0000102mm,用科学记数法表示为( )
| A. | 1.02×10-5mm | B. | 10.2×10-6mm | C. | 102×10-4mm | D. | 102×10-8mm |